题目内容
4.已知关于x的方程$\frac{2x+m}{x-2}$=3的解是正数,则m的取值范围是m>-6且m≠-4.分析 首先求出关于x的方程$\frac{2x+m}{x-2}$=3的解,然后根据解是正数,再解不等式求出m的取值范围.
解答 解:解关于x的方程$\frac{2x+m}{x-2}$=3得x=m+6,
∵方程的解是正数,
∴m+6>0且x-2≠0,即m+6≠2,
解得:m>-6且m≠-4.
故答案为:m>-6且m≠-4.
点评 本题考查了分式方程的解,是一个方程与不等式的综合题目,解关于x的方程是前提,得到关于x的不等式是本题的关键.

练习册系列答案
相关题目
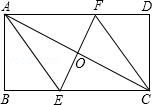 如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.
如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.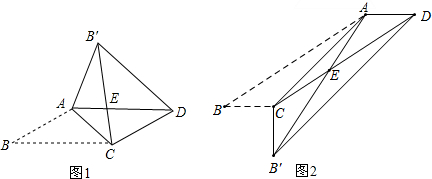
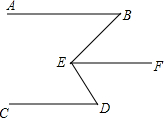 如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?
如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?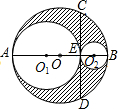 如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).
如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).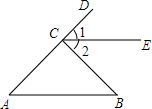 如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.
如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.