题目内容
8.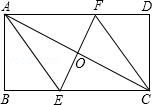 如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.
如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.(1)求证:四边形AECF是菱形;
(2)若AB=4,BC=8,求菱形AECF的面积.
分析 (1)由折叠的性质可得:OA=OC,EF⊥AC,即可证得AF=CF,又由四边形ABCD是矩形,易证得△AOF≌△COE,可得OE=OF,继而可证得四边形AECF是菱形;
(2)首先设CE=x,则AE=x,be=8-x,然后由勾股定理求得(8-x)2+42=x2,继而求得答案.
解答 (1)证明:由折叠的性质可得:OA=OC,EF⊥AC,
∴AF=CF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAC=∠ECA,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠FAC=∠ECA}\\{OA=OC}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴OE=OF,
∴四边形AECF是平行四边形,
∵AF=CF,
∴四边形AECF是菱形;
(2)解:设CE=x,则AE=x,be=8-x,
∵四边形ABCD是矩形,
∴∠B=90°,
∴BE2+AB2=AE2,
∴(8-x)2+42=x2,
解得:x=5,即EC=5,
∴S菱形AECF=EC•AB=5×4=20.
点评 此题考查了折叠的性质、矩形的性质、菱形的判定与性质以及勾股定理.注意掌握折叠前后图形的对应关系是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.x取下列各数中的哪个数时,二次根式$\sqrt{x-5}$有意义( )
| A. | -3 | B. | 0 | C. | 3 | D. | 6 |
3. 某中学计划成立多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计表(不完整):
某中学计划成立多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计表(不完整):
某校被调查学生选择社团意向统计表
根据统计图表中的信息,解答下列问题:
(1)请直接写出本次调查的总人数以及a和b的值;
(2)将条形统计图补充完整.
 某中学计划成立多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计表(不完整):
某中学计划成立多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计表(不完整):某校被调查学生选择社团意向统计表
| 选择意向 | 文学欣赏 | 科学实验 | 音乐艺术 | 手工制作 | 体育运动 | 其他 |
| 所占百分比 | a | 22.5% | b | 10% | 20% | 2.5% |
(1)请直接写出本次调查的总人数以及a和b的值;
(2)将条形统计图补充完整.
13.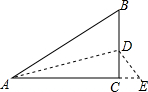 如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
 如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |

 一次函数y=kx+b(k,b是常数,k≠0)图象如图所示,则不等式kx+b>0的解集是x>-2.
一次函数y=kx+b(k,b是常数,k≠0)图象如图所示,则不等式kx+b>0的解集是x>-2.