题目内容
5.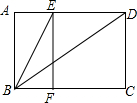 如图所示,已知矩形ABCD与矩形AEFB相似,连接BE,BD,则下列判断中:
如图所示,已知矩形ABCD与矩形AEFB相似,连接BE,BD,则下列判断中:①$\frac{{S}_{矩形AEFB}}{{S}_{矩形ABCD}}$=$\frac{{AB}^{2}}{{AD}^{2}}$;②$\frac{{S}_{矩形AEFB}}{{S}_{矩形ABCD}}$=$\frac{AE}{AD}$;③△AEB∽△ABD;④∠BEF=∠DBC.
其中正确的是①③④.(选填序号)
分析 依据相似三角形的面积比等于相似比的平方可判断①、②;依据有两组对应边成比例且夹角相等的两三角形相似进行判断即可;依据相似三角形的性质和平行线的性质可判断.
解答 解:∵相似三角形的面积比等于相似比的平方,
∴①正确;②错误.
∵矩形ABCD与矩形AEFB相似,
∴$\frac{AE}{AB}=\frac{AB}{AD}$.
又∵∠A=∠A,
∴△AEB∽△ABD.故③正确.
∵△AEB∽△ABD,
∴∠ABE=∠ADB.
又∵∠ABE=∠BEF,∠ADB=∠DBC,
∴∠BEF=∠DBC,故④正确.
故答案为:①③④.
点评 本题主要考查的是相似多边形的性质、相似三角形的性质和判定,掌握相似多边形的性质、相似三角形的性质和判定定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.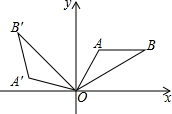 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )| A. | (-2,2$\sqrt{2}$) | B. | (-2$\sqrt{2}$,2) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
17.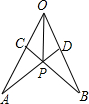 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
15.若$\frac{|x|-2}{{x}^{2}-x-2}$=0,则x等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
 已知,∠α
已知,∠α 在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.
在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.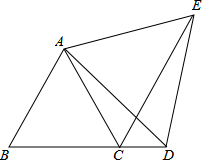 如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.
如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.