题目内容
17.已知关于x的二次方程x2+mx+2m-n=0有两个相等的实数根2,求m,n的值.分析 将x=2代入原方程,可得出n=4m+4,再根据方程有两个相等的实数根结合根的判别式,可得出m2-8m+4n=0,将n=4m+4代入m2-8m+4n=0,可求出m值,进而即可得出n的值,此题得解.
解答 解:∵2是方程x2+mx+2m-n=0的根,
∴22+2m+2m-n=0,
即n=4m+4.
又∵方程x2+mx+2m-n=0有两个相等的实数根,
∴△=m2-4(2m-n)=0,即m2-8m+4n=0.
将n=4m+4代入m2-8m+4n=0得:m2+8m+16=0.
解得:m=-4,
∴n=4m+4=-12.
点评 本题考查了根的判别式以及一元二次方程的解,根据一元二次方程的解以及根的判别式找出m、n之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.关于x的一元二次方程x2-kx-6=0的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定根的情况 |
6.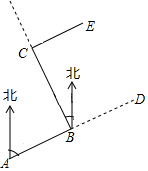 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 105° |




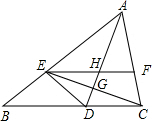 如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.