题目内容
8.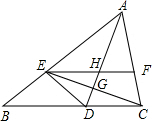 如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
分析 (1)根据等腰三角形三线合一的性质即可证明AD垂直平分CE;
(2)由(1)可知点D为CE垂直平分线上的点,则CD=DE,∠DCE=∠DEC.由EF∥BC,可得∠DCE=∠CEF=∠DEC,则EG平分∠DEF.再证明∠EDH=∠EHD,然后由∠BCE=40°,得出∠DEH=2∠BCE=80°,进而求出∠EHD=$\frac{1}{2}$(180°-80°)=50°.
解答 (1)证明:∵AE=AC,AD是∠BAC平分线,
∴AD垂直平分CE; (2)解:由(1)可知点D为CE垂直平分线上的点,
(2)解:由(1)可知点D为CE垂直平分线上的点,
∴CD=DE,
∴∠DCE=∠DEC.
∵EF∥BC,
∴∠DCE=∠CEF=∠DEC,
∴EG平分∠DEF.
∵EG⊥AD,
∴△DEH是等腰三角形,且ED=EH,
∴∠EDH=∠EHD,
∵∠BCE=40°,
∴∠DEH=2∠BCE=80°,
∴∠EHD=$\frac{1}{2}$(180°-80°)=50°.
点评 本题考查了等腰三角形的性质,线段垂直平分线的性质,平行线的性质,三角形内角和定理,掌握性质与定理是解题的关键.

练习册系列答案
相关题目
18. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5°
④BC+FG=1.5,其中正确的结论是( )
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5°
④BC+FG=1.5,其中正确的结论是( )
| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ② |
13.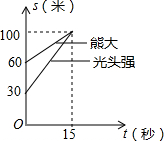 在动画片《熊出没》中,有一次光头强追赶熊大,在距离光头强家100米的地方追上了熊大,下图反映了这一过程,其中s表示光头强家的距离,t表示光头强追赶的时间,根据相关信息,以下说法错误的是( )
在动画片《熊出没》中,有一次光头强追赶熊大,在距离光头强家100米的地方追上了熊大,下图反映了这一过程,其中s表示光头强家的距离,t表示光头强追赶的时间,根据相关信息,以下说法错误的是( )
 在动画片《熊出没》中,有一次光头强追赶熊大,在距离光头强家100米的地方追上了熊大,下图反映了这一过程,其中s表示光头强家的距离,t表示光头强追赶的时间,根据相关信息,以下说法错误的是( )
在动画片《熊出没》中,有一次光头强追赶熊大,在距离光头强家100米的地方追上了熊大,下图反映了这一过程,其中s表示光头强家的距离,t表示光头强追赶的时间,根据相关信息,以下说法错误的是( )| A. | 开始熊大与光头强之间的距离是30米 | |
| B. | 光头强跑了60米追上熊大 | |
| C. | 15秒后光头强追上了熊大 | |
| D. | 光头强追上熊大时,熊大跑了40米 |
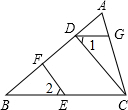 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上. 如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.
如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.