题目内容
9.在Rt△ABC中,∠ACB=90°,AC=BC,O是AB边的中点,D、E分别在AC、BC上,∠EOD=90°,DF∥BC交AB于点F,连接EF、OC.(1)如图1,求证:四边形DCEF是矩形;
(2)如图2,若∠COE=22.5°,写出图中长度等于EF的线段.(CD除外)

分析 (1)根据直角三角形的性质得到CO=$\frac{1}{2}$AB=AO=BO,根据等腰直角三角形的性质得到∠A=∠B=45°,OC⊥AB,∠ACO=∠BCO=45°,推出∠AOD=∠COE,根据全等三角形的性质得到AD=CE,根据平行线的性质得到∠ADF=90°,推出DF=AD=CE,得到四边形DCEF是平行四边形,于是得到结论;
(2)由江西的性质得到EF⊥BC,推出△BEF是等腰直角三角形,得到EF=BE,根据等腰三角形的判定即可得到结论.
解答 (1)证明:∵∠ACB=90°,O是AB边的中点,
∴CO=$\frac{1}{2}$AB=AO=BO,
∵AC=BC,
∴∠A=∠B=45°,OC⊥AB,∠ACO=∠BCO=45°,
∴∠A=∠BCO,
∵∠EOD=90°,
∴∠AOD+∠DOC=∠COE+∠DOC,
∴∠AOD=∠COE,
在△ADO与△CEO中,$\left\{\begin{array}{l}{∠A=∠OCE}\\{AO=CO}\\{∠AOD=∠COE}\end{array}\right.$,
∴△ADO≌△CEO,
∴AD=CE,
∵DF∥BC,
∴∠ADF=90°,
∴∠AFD=∠A=45°,
∴DF=AD=CE,
∴四边形DCEF是平行四边形,
∵∠ACB=90°,
∴四边形DCEF是矩形;
(2)解:∵四边形DCEF是矩形;
∴EF⊥BC,
∴△BEF是等腰直角三角形,
∴EF=BE,
∵∠COE=22.5°,
∴∠EOB=67.5°,
∴∠OEB=67.5°,
∴∠BOE=∠BEO,
∴BE=BO,
∴EF=BE=BO=AO=CO,
∴图中长度等于EF的线段是BE,BO,AO,CO.
点评 本题考查了矩形的判定和性质,全等三角形的判定和性质,平行线的性质,等腰直角三角形的判定和性质,熟练掌握各定理是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案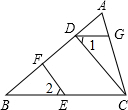 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.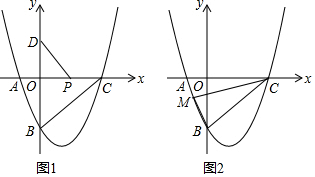
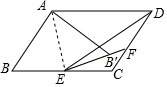 如图,?ABCD中,E为BC上一点,将?ABCD沿AE折叠,点B落在点B′处,EB′的延长线交CD于F,EF=DF,若∠B=60°,∠BAE=40°,则∠CDE的度数为20°.
如图,?ABCD中,E为BC上一点,将?ABCD沿AE折叠,点B落在点B′处,EB′的延长线交CD于F,EF=DF,若∠B=60°,∠BAE=40°,则∠CDE的度数为20°.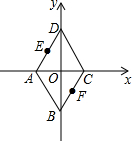 以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,AD的中点E的坐标为(-1,2),则BC的中点F的坐标为(1,-2).
以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,AD的中点E的坐标为(-1,2),则BC的中点F的坐标为(1,-2).