��Ŀ����
5���Ķ����ϲ�������⣺$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{��\sqrt{2}+1����\sqrt{2}-1��}$=$\frac{\sqrt{2}-1}{��{\sqrt{2}��}^{2}-{1}^{2}}$=$\sqrt{2}$-1����������������У�$\sqrt{2}$+1��$\sqrt{2}$-1��˵Ļ��������θ�ʽ�����ǿ��Խ�������ʽ�ӳ�Ϊ��Ϊ��������ʽ�������������Ҳ��Ϊ��ĸ����������1��������ʽ�ӽ��з�ĸ����������$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$����$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$��
��2������$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$��
���� �������⼴�ɽ��з�ĸ������
��� �⣺��1��$\frac{\sqrt{3}}{3}$��$\sqrt{3}$+$\sqrt{2}$
��2��ԭʽ=$\frac{\sqrt{3}-1}{��\sqrt{3}+1����\sqrt{3}-1��}$+$\frac{\sqrt{5}-\sqrt{3}}{��\sqrt{5}+\sqrt{3}����\sqrt{5}-\sqrt{3}��}$
=$\frac{\sqrt{3}-1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}$
=$\frac{\sqrt{5}-1}{2}$
�ʴ�Ϊ����1��$\frac{\sqrt{3}}{3}$��$\sqrt{3}$+$\sqrt{2}$
���� ���⿼���ĸ������������Ĺؼ�����ȷ�����⣬��������ƽ���ʽ���������ڻ������ͣ�

��ϰ��ϵ�д�
�����Ŀ
15��������Ϊx������Ϊy��������3����������һ����2���гɷ����ǣ�������
| A�� | 3x+$\frac{1}{2}$y=2 | B�� | 3x-$\frac{1}{2}$y=2 | C�� | -3x+$\frac{1}{2}$y=2 | D�� | 3x=$\frac{1}{2}$y+2 |
13��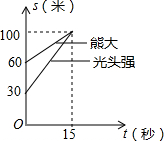 �ڶ���Ƭ���ܳ�û���У���һ�ι�ͷǿ���ܴ��ھ����ͷǿ��100�ĵط������ܴ���ͼ��ӳ����һ���̣�����s��ʾ��ͷǿ�ҵľ��룬t��ʾ��ͷǿ�ϵ�ʱ�䣬���������Ϣ������˵��������ǣ�������
�ڶ���Ƭ���ܳ�û���У���һ�ι�ͷǿ���ܴ��ھ����ͷǿ��100�ĵط������ܴ���ͼ��ӳ����һ���̣�����s��ʾ��ͷǿ�ҵľ��룬t��ʾ��ͷǿ�ϵ�ʱ�䣬���������Ϣ������˵��������ǣ�������
 �ڶ���Ƭ���ܳ�û���У���һ�ι�ͷǿ���ܴ��ھ����ͷǿ��100�ĵط������ܴ���ͼ��ӳ����һ���̣�����s��ʾ��ͷǿ�ҵľ��룬t��ʾ��ͷǿ�ϵ�ʱ�䣬���������Ϣ������˵��������ǣ�������
�ڶ���Ƭ���ܳ�û���У���һ�ι�ͷǿ���ܴ��ھ����ͷǿ��100�ĵط������ܴ���ͼ��ӳ����һ���̣�����s��ʾ��ͷǿ�ҵľ��룬t��ʾ��ͷǿ�ϵ�ʱ�䣬���������Ϣ������˵��������ǣ�������| A�� | ��ʼ�ܴ����ͷǿ֮��ľ�����30�� | |
| B�� | ��ͷǿ����60�����ܴ� | |
| C�� | 15����ͷǿ�����ܴ� | |
| D�� | ��ͷǿ���ܴ�ʱ���ܴ�����40�� |
 ��ͼ���ڡ�ABC�У���ACB=90�㣬D��E��F�ֱ���AC��AB��BC���е㣮
��ͼ���ڡ�ABC�У���ACB=90�㣬D��E��F�ֱ���AC��AB��BC���е㣮
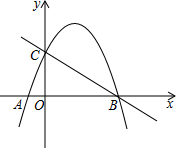 ��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{3}{4}$x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C��ֱ��y=-$\frac{3}{4}$x+3����B��C���㣮
��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{3}{4}$x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C��ֱ��y=-$\frac{3}{4}$x+3����B��C���㣮 ��ֱ�������з���������y=$\frac{6}{x}$��ͼ����ͼ��ʾ��
��ֱ�������з���������y=$\frac{6}{x}$��ͼ����ͼ��ʾ��