Question

1．解不等式组$\left\{\begin{array}{l}{2x+3≤1}\\{x＞\frac{1}{2}（x-3）}\end{array}\right.$的解集在数轴上表示正确的是（　　）

• A．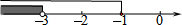
• B．
• C．
• D．

Answer 1

分析 分别求得不等式组中的两个不等式的解集，然后取其交集，并表示在数轴上．

解答 解：$\left\{\begin{array}{l}{2x+3≤1（1）}\\{x＞\frac{1}{2}（x-3）（2）}\end{array}\right.$
解不等式（1），得
x≤-1．
解不等式（2），得
x＞-3，
则原不等式组的解集为：-3＜x≤-1．
表示在数轴上为：．
故选：C．

点评 本题考查了解不等式组，在数轴上表示不等式的解集．把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．