题目内容

10．先化简，再求值：（$\frac{x}{x-1}$-$\frac{x-1}{x}$）÷$\frac{2x-1}{{x}^{2}+x}$，其中x=3．

分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．

解答 解：原式=$\frac{{x}^{2}-（x-1）^{2}}{x（x-1）}$•$\frac{x（x+1）}{2x-1}$=$\frac{2x-1}{x（x-1）}$•$\frac{x（x+1）}{2x-1}$=$\frac{x+1}{x-1}$，
当x=3时，原式=2．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
20．解方程组$\left\{\begin{array}{l}{x+y+z=36\\;①}\\{x-y=1\\;②}\\{2x+z-y=18\\;③}\end{array}\right.$时，把①+②，可立即得到一个二元一次方程2x+z=37．
1．解不等式组$\left\{\begin{array}{l}{2x+3≤1}\\{x＞\frac{1}{2}（x-3）}\end{array}\right.$的解集在数轴上表示正确的是（　　）
A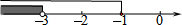．B．
C．D．
18．解方程：$\frac{x}{x+3}-\frac{2}{x}$=1．
5．已知k、b是一元二次方程（2x+1）（3x-1）=0的两个根，且k＞b，则函数y=kx+b的图象不经过（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
15．若-2x3ym与5xny2是同类项，则m=2，n=3．
2．如图1：在平面直角坐标系xOy中，M为x轴正半轴上一点，⊙M与x轴交于A、B两点，与 y轴交于C、D两点，若点M的坐标为（2，0），B点的坐标为（6，0）．
（1）求C点的坐标；
（2）如图2连接AC，若E为⊙M上一点，且弦AE长为$4\sqrt{2}$，求∠EAC的度数．
（3）如图3：K、L分别为 $\widehat{BC}$、$\widehat{BD}$上的动点，连接AK，BC交于点R，AL、BD交于点G，若∠KAL=60°  现给出两个结论：①△ARG的周长不变；②△BRG的周长不变．其中有一个结论正确，请选择正确结论并求值．
19．已知如图，抛物线与y轴交于A（0，-2），与x轴交于B（-2，0），C（2，0），直线y=x与抛物线交于点D，点P在直线y=x上运动．
（1）求抛物线的解析式和点D的坐标；
（2）当点P的横坐标为$\sqrt{2}$，试求∠APB的度数；
（3）是否存在点P，使得以A、C、D、P为顶点的四边形为平行四边形？若存在，求点P的坐标；若不存在说明理由；
（4）当∠APB的度数为135°，直接写出点P的坐标．
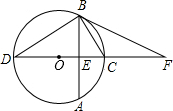20．如图，⊙O的直径CD垂直于弦AB，垂足为E，F为DC延长线上一点，且∠CBF=∠CDB．
（1）求证：FB为⊙O的切线；
（2）若AB=8，CE=2，求sin∠BDC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网