题目内容
13.函数y=$\frac{\sqrt{1-2x}}{x}$的自变量x的取值范围是x≤$\frac{1}{2}$且x≠0.分析 根据分母不为零和被开方数不小于零得到x≠0且1-2x≥0,然后求出两不等式的公共解即可.
解答 解:根据题意得x≠0且1-2x≥0,
所以x≤$\frac{1}{2}$且x≠0.
故答案为
点评 本题考查了函数自变量的取值范围:自变量的取值范围必须使含有自变量的表达式都有意义,当表达式的分母中含有自变量时,自变量取值要使分母不为零;当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.

练习册系列答案
相关题目
3.为了了解萧山区2014年数学学业考试各分数段成绩分布情况,从中抽取 1500名考生的学业考试数学成绩进行统计分析.在这个问题中,样本容量是指( )
| A. | 1500 | |
| B. | 被抽取的1500名考生 | |
| C. | 被抽取的1500名考生的学业考试数学成绩 | |
| D. | 义乌市2013年学业考试数学成绩 |
1.解不等式组$\left\{\begin{array}{l}{2x+3≤1}\\{x>\frac{1}{2}(x-3)}\end{array}\right.$的解集在数轴上表示正确的是( )
| A. | 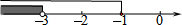 | B. |  | ||
| C. |  | D. |  |
5.已知k、b是一元二次方程(2x+1)(3x-1)=0的两个根,且k>b,则函数y=kx+b的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.把直线y=-x+l沿y轴向上平移一个单位,得到新直线的关系式是( )
| A. | y=-x | B. | y=-x+2 | C. | y=-x-2 | D. | y=-2x |