题目内容
14.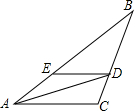 如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
分析 先证明∠EAD=∠EDA得到EA=ED=4,再利用平行线分线段成比例定理得到$\frac{BE}{AE}$=$\frac{BD}{CD}$,然后利用比例的性质可求出BE的长.
解答 解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠EDA,
∴∠EAD=∠EDA,
∴EA=ED=4,
∵DE∥AC,
∴$\frac{BE}{AE}$=$\frac{BD}{CD}$,
而DC=$\frac{1}{3}$BC,
∴BE=2AE=8.
故答案为8.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了等腰三角形的性质.

练习册系列答案
相关题目
5.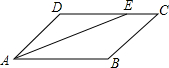 如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )
如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )
 如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )
如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0.5 |
2.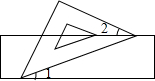 如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )
如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )
 如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )
如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )| A. | 25° | B. | 20° | C. | 15° | D. | 30° |
9.下列方程中,有两个相等的实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-1=0 |
4.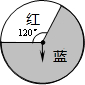 一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
 一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )| A. | 转出的结果一定是“蓝色” | |
| B. | 转出的结果为“蓝色”的可能性大于“红色” | |
| C. | 转出的结果为“红色”的可能性大于“蓝色” | |
| D. | 转出的结果为“蓝色”和“红色”的可能性一样大 |
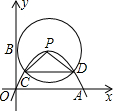 如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).
如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).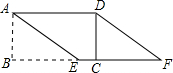 如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.