题目内容
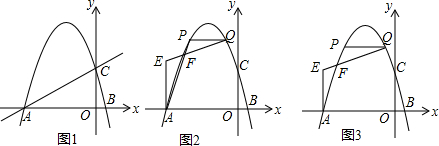
19.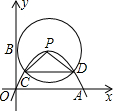 如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).
如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).
分析 过P作PE⊥OA于E,根据已知条件得到OE=$\frac{1}{2}$OA=$\frac{1}{2}$m,连接PB,根据切线的性质得到PB⊥OB,推出四边形PBOE是矩形,根据矩形的性质得到PB=OE=$\frac{1}{2}$m,根据圆的性质得到PC=PD=PB=$\frac{1}{2}$m,于是得到结论.
解答 解:过P作PE⊥OA于E,
∵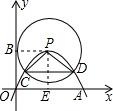 P为抛物线的顶点,
P为抛物线的顶点,
∴OE=$\frac{1}{2}$OA=$\frac{1}{2}$m,
连接PB,
∵⊙P与y轴相切于点B,
∴PB⊥OB,
∴四边形PBOE是矩形,
∴PB=OE=$\frac{1}{2}$m,
∴PC=PD=PB=$\frac{1}{2}$m,
∴△PCD的周长为=PC+PD+CD=m+n,
故答案为:m+n.
点评 本题考查了切线的性质,二次函数图象上点的坐标特征,圆的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
9. 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )
 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
4.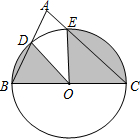 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )| A. | $\frac{64}{9}π$ | B. | $\frac{32}{9}π$ | C. | $\frac{16}{9}π$ | D. | $\frac{8}{9}π$ |
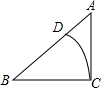 如图,Rt△ABC中,∠C=90°,∠A=50°,BC=3,以点B为圆心,BC为半径作弧,交AB于点D,则$\widehat{CD}$的长为$\frac{2π}{3}$.
如图,Rt△ABC中,∠C=90°,∠A=50°,BC=3,以点B为圆心,BC为半径作弧,交AB于点D,则$\widehat{CD}$的长为$\frac{2π}{3}$. 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.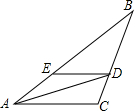 如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
 如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.
如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.