题目内容
3.三角形的三边分别为a,b,c,且(a-b)2+(a2+b2-c2)2=0,则三角形的形状为等腰直角三角形.分析 由于(a-b)2+(a2+b2-c2)2=0,利用非负数的性质可得a=b,且a2+b2=c2,根据等腰三角形的定义以及勾股定理的逆定理可得以a,b,c为边的三角形是等腰直角三角形.
解答 解:∵(a-b)2+(a2+b2-c2)2=0,
∴a-b=0,且a2+b2-c2=0,
∴a=b,且a2+b2=c2,
∴以a,b,c为边的三角形是等腰直角三角形.
故答案为等腰直角三角形.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了等腰三角形的定义以及非负数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.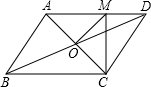 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )| A. | 40cm | B. | 60cm | C. | 70cm | D. | 80cm |
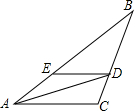 如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=$\frac{1}{3}$BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为8.
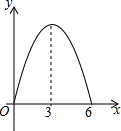
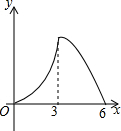
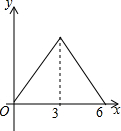
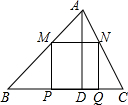 锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )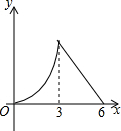
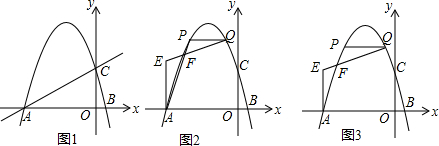
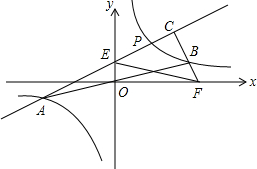 已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.
已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.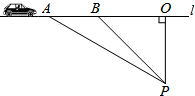 超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?
超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?