题目内容
 如图,△ABC的二条高AD,CF相交于点H,D,F分别为垂足,AD的延长线交△ABC的外接圆于点E,求证:HD=DE.
如图,△ABC的二条高AD,CF相交于点H,D,F分别为垂足,AD的延长线交△ABC的外接圆于点E,求证:HD=DE.考点:圆周角定理,全等三角形的判定与性质
专题:证明题
分析:连结CE,如图,利用等角的余角相得到∠1=∠3,再根据圆周角定理得到∠2=∠3,则∠1=∠2,加上CD⊥HE,则可判断△CEH为等腰三角形,然后根据等腰三角形的性质得HD=DE.
解答:证明:连结CE,如图,
∵AD和CF为△ABC的高,
∴∠1+∠B=90°,∠3+∠B=90°,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
而CD⊥HE,
∴△CEH为等腰三角形,
∴HD=DE.

∵AD和CF为△ABC的高,
∴∠1+∠B=90°,∠3+∠B=90°,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
而CD⊥HE,
∴△CEH为等腰三角形,
∴HD=DE.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的判定与性质.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
某工厂计划从2013年到2015两年间,把某商品的售价从289元降低为256元,设平均每次降价的百分率为x,则可列方程是( )
| A、256(1+x)2=289 |
| B、289(1-x)2=256 |
| C、289(1-x2)=256 |
| D、256(1+x 2)=289 |
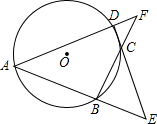 如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )
如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )| A、30° | B、40° |
| C、57° | D、70° |
 如图,平行四边形ABOC中,A(2,1),B(4,-3),求点C的坐标.
如图,平行四边形ABOC中,A(2,1),B(4,-3),求点C的坐标. 如图,在△ABC中.AB=AC,AB的垂直平分线交直线AB于点N,交直线BC于点M.若∠A=40°,求∠NMB的大小.
如图,在△ABC中.AB=AC,AB的垂直平分线交直线AB于点N,交直线BC于点M.若∠A=40°,求∠NMB的大小.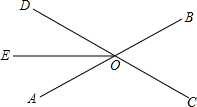 如图,直线AB,CD相交于点O,OE平分∠AOD,∠BOC=∠BOD-30°,求∠COE的度数.
如图,直线AB,CD相交于点O,OE平分∠AOD,∠BOC=∠BOD-30°,求∠COE的度数.