题目内容
 如图,平行四边形ABOC中,A(2,1),B(4,-3),求点C的坐标.
如图,平行四边形ABOC中,A(2,1),B(4,-3),求点C的坐标.考点:平行四边形的性质,坐标与图形性质
专题:
分析:过C作CZ⊥x轴于Z,过A作AM⊥CZ轴于M,交OC于N,过B作BQ⊥AM于Q,证△CZO≌△BQA,推出CZ=BQ,AQ=ZO,根据A、B的坐标求出AQ和BQ即可.
解答: 解:过C作CZ⊥x轴于Z,过A作AM⊥CZ轴于M,交OC于N,过B作BQ⊥AM于Q,
解:过C作CZ⊥x轴于Z,过A作AM⊥CZ轴于M,交OC于N,过B作BQ⊥AM于Q,
则AM∥x轴,∠CZO=∠Q=90°,
∵四边形ABOC是平行四边形,
∴AB=OC,AB∥OC,
∴∠QAB=∠EAM=∠CNM=∠COZ,
在△CZO和△BQA中,
,
∴△CZO≌△BQA(AAS),
∴CZ=BQ,OZ=AQ,
∵A(2,1),B(4,-3),
∴CZ=BQ=1+3=4,OZ=AQ=4-2=2,
即C的坐标是(-2,4).
 解:过C作CZ⊥x轴于Z,过A作AM⊥CZ轴于M,交OC于N,过B作BQ⊥AM于Q,
解:过C作CZ⊥x轴于Z,过A作AM⊥CZ轴于M,交OC于N,过B作BQ⊥AM于Q,则AM∥x轴,∠CZO=∠Q=90°,
∵四边形ABOC是平行四边形,
∴AB=OC,AB∥OC,
∴∠QAB=∠EAM=∠CNM=∠COZ,
在△CZO和△BQA中,
|
∴△CZO≌△BQA(AAS),
∴CZ=BQ,OZ=AQ,
∵A(2,1),B(4,-3),
∴CZ=BQ=1+3=4,OZ=AQ=4-2=2,
即C的坐标是(-2,4).
点评:本题考查了平行四边形的性质,坐标与图形性质,全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线,题目比较好,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,则它有几种路径?获得食物的概率是多少?
一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,则它有几种路径?获得食物的概率是多少? 如图,△AOB中,∠O=90°,AB=5cm,OA=4cm.
如图,△AOB中,∠O=90°,AB=5cm,OA=4cm. 如图,△ABC的二条高AD,CF相交于点H,D,F分别为垂足,AD的延长线交△ABC的外接圆于点E,求证:HD=DE.
如图,△ABC的二条高AD,CF相交于点H,D,F分别为垂足,AD的延长线交△ABC的外接圆于点E,求证:HD=DE.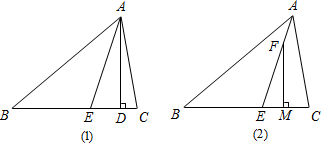
 已知OE是∠BOC的平分线,且∠AOE=90°,∠AOC=110°,则∠BOC=
已知OE是∠BOC的平分线,且∠AOE=90°,∠AOC=110°,则∠BOC=