题目内容
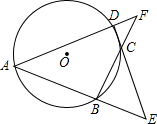 如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )
如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )| A、30° | B、40° |
| C、57° | D、70° |
考点:圆内接四边形的性质,三角形内角和定理
专题:
分析:根据三角形内角和定理以及圆内接四边形内对角的和为180°,进而得出2∠A+∠E+∠F=180°,进而求出即可.
解答:解:∵在△ABF和△ADE中
∠A+∠ABF+∠F=180°,∠A+∠E+∠ADE=180°,
∴∠A+∠ABF+∠F+∠A+∠E+∠ADE=180°+180°=360°,
∵∠ADE+∠ABF=180°,
∴2∠A+∠E+∠F=180°,
∴2∠A=180°-36°-30°=114°,
∴∠A=57°.
故选:C.
∠A+∠ABF+∠F=180°,∠A+∠E+∠ADE=180°,
∴∠A+∠ABF+∠F+∠A+∠E+∠ADE=180°+180°=360°,
∵∠ADE+∠ABF=180°,
∴2∠A+∠E+∠F=180°,
∴2∠A=180°-36°-30°=114°,
∴∠A=57°.
故选:C.
点评:此题主要考查了圆内接四边形的性质以及三角形内角和定理等知识,得出2∠A+∠E+∠F=180°是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
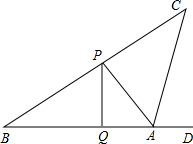 AC是一条不能行走的斜坡,为了测量斜坡AC的长度,在一次课外实践活动中.小明所在的活动小组进行了以下的操作:首先在AB之间插一根12米高的旗杆PQ,他们在B处测得旗杆顶点P的仰角为30°,在A处测得旗杆顶点P的仰角为45°,在A处测得斜坡的末端C点的仰角为75°.
AC是一条不能行走的斜坡,为了测量斜坡AC的长度,在一次课外实践活动中.小明所在的活动小组进行了以下的操作:首先在AB之间插一根12米高的旗杆PQ,他们在B处测得旗杆顶点P的仰角为30°,在A处测得旗杆顶点P的仰角为45°,在A处测得斜坡的末端C点的仰角为75°. 如图所示,已知△ABC中,BD:DC=3:2,AF:FD=2:1,求AE:EC.
如图所示,已知△ABC中,BD:DC=3:2,AF:FD=2:1,求AE:EC. 如图,△ABC的二条高AD,CF相交于点H,D,F分别为垂足,AD的延长线交△ABC的外接圆于点E,求证:HD=DE.
如图,△ABC的二条高AD,CF相交于点H,D,F分别为垂足,AD的延长线交△ABC的外接圆于点E,求证:HD=DE. 如图,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求出∠A+∠B+∠C+∠D+∠E+∠F的度数. 如图,在△ABC中,如果∠AGD=∠ACB,CD⊥AB,EF⊥AB,那么∠1=∠2吗?试说明理由.
如图,在△ABC中,如果∠AGD=∠ACB,CD⊥AB,EF⊥AB,那么∠1=∠2吗?试说明理由.