题目内容
14.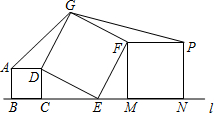 在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
分析 作GH⊥AD交AD的延长线于H,首先证明△DHG≌△DCE,再证明S△ADG=S△DCE,求出△DCE的面积即可.
解答 解: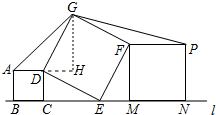 作GH⊥AD交AD的延长线于H,
作GH⊥AD交AD的延长线于H,
∵∠HDC=∠GDE=90°,
∴∠GDH=∠CDE,
在△DHG和△DCE中,
$\left\{\begin{array}{l}{∠H=∠DCE=90°}\\{∠GDH=∠CDE}\\{DG=DE}\end{array}\right.$,
∴△DHG≌△DCE,
∴GH=CE,
∵S△ADG=$\frac{1}{2}$•DA•GH,S△DCE=$\frac{1}{2}$•DC•CE,
∵AD=CD,GH=EC,
∴S△ADG=S△DCE,
∵CD2=4,DE2=13
∴CD=2,CE=$\sqrt{D{E}^{2}-D{C}^{2}}$=3,
∴S△ADG=S△DCE=$\frac{1}{2}$•CD•CE=3.
故答案为3.
点评 本题考查全等三角形的判定和性质、正方形的性质、以及三角形的面积公式,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
7.在?ABCD中,对角线AC和BD相交于点O,若AC=8,BD=6,则AB的长不可能是( )
| A. | 1 | B. | 2 | C. | 5 | D. | 6 |
19.下列各式正确的是( )
| A. | -(+8)=8 | B. | -(-3)=-3 | C. | -$\frac{2}{3}$<-$\frac{1}{2}$ | D. | -π>-3.14 |
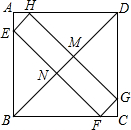 如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.
如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.