题目内容
2.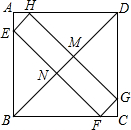 如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.
如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.
分析 先证明△AEH,△CFG都是等腰直角三角形,证明△AEH≌△CFG得AE=AH=FC=CG,根据EH=$\sqrt{2}$AE,EF=$\sqrt{2}$EB,得EF+EH=$\sqrt{2}$AB由此即可解决问题.
解答 解:∵EH∥FG,且EH=FG,
∴四边形EFGH是平行四边形,
又∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABD=45°, ∠A=∠C=∠ABC=90°
∠A=∠C=∠ABC=90°
∵EH∥BD,
∴∠AEH=∠ABD=∠AHE=45°,
同理∠GFC=∠FGC=45°,
在△AEH和△CFG中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠AEH=∠CFG}\\{EH=FG}\end{array}\right.$,
∴△AEH≌△CFG,
∴AE=CF=AH=CG,
∴BE=EF,
∵EH=$\sqrt{2}$AE,EF=$\sqrt{2}$BE,
∴EH+EF=$\sqrt{2}$(AE+EB)=$\sqrt{2}$AB,
∵EH+EF=$\sqrt{2}$a,
∴AB=a,
∴正方形周长为4a.
故答案为4a.
点评 本题考查正方形的性质、全等三角形的判定和性质、平行四边形的判定和性质,解题关键是利用三角形全等,学会利用特殊三角形的边之间的关系解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.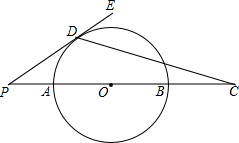 如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )
如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )
 如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )
如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{13}}{13}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{13}}{13}$ |
11.已知数据x1,x2,x3的平均数是5,则数据3x1+2,3x2+2,3x3+2的平均数是( )
| A. | 5 | B. | 7 | C. | 15 | D. | 17 |
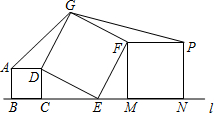 在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$. 如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.