题目内容
3.先化简,再求值:x-2-$\frac{x^2}{x+2}$,其中x=2$\sqrt{2}$-2.分析 先通分,再算减法,化成最简,最后把x=2$\sqrt{2}$-2代入计算即可.
解答 解:原式=$\frac{(x+2)(x-2)}{x+2}$-$\frac{{x}^{2}}{x+2}$
=$\frac{{x}^{2}-4}{x+2}$-$\frac{{x}^{2}}{x+2}$
=$\frac{{x}^{2}-4-{x}^{2}}{x+2}$
=-$\frac{4}{x+2}$,
当x=2$\sqrt{2}$-2时,
原式=-$\frac{4}{2\sqrt{2}-2+2}$
=-$\frac{4}{2\sqrt{2}}$
=-$\sqrt{2}$.
点评 本题考查了分式的化简求值,特别注意运算顺序及符号的处理,也需要对通分、分解因式、约分等知识点熟练掌握.

练习册系列答案
相关题目
11.已知数据x1,x2,x3的平均数是5,则数据3x1+2,3x2+2,3x3+2的平均数是( )
| A. | 5 | B. | 7 | C. | 15 | D. | 17 |
13.下列四幅图案在设计中用到平移变换方式的是( )
| A. |  | B. |  | C. |  | D. |  |
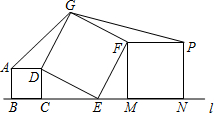 在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$. 如图,以O为位似中心,将△ABC放大为原来的2倍.
如图,以O为位似中心,将△ABC放大为原来的2倍. 如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.