题目内容
9.我们常常用符号f(x)表示x的函数,例如函数f(x)=x2-2x+1,则f(3)=32-2x+1=4.对于函数f(x),若存在a,b,f(x)满足以下条件:
①当a<x<x0时,随着x的增大,函数值f(x)增大;
②当x0<x<b时,随着x的增大,函数值f(x)减小,则称f(x0)为f(x)的一个峰值.
(1)判断函数f(x)=x+1是否具有峰值;
(2)求函数f(x)=x2+4x+1的峰值;
(3)已知m为非零实数,当x≤m时,函数y=m(x-1)2+2m2的图象记为T1:当x>m时,函数y=(m2-1)x+2m的图象记为T2:图象T1,T2组成图象T.图象T所对应的函数记为f(x),若f(x)存在峰值,求实数m的取值范围.
分析 (1)由一次函数的性质可知函数f(x)=x+1在其值域内单调递增,故不存在峰值;
(2)结合二次函数的性质可知,抛物线的顶点为它的峰值;
(3)结合系数的关系,可将整个x的取值分五段考虑,结合一次函数与二次函数的性质和图象即可得出结论.
解答 解:(1)函数f(x)=x+1在其值域内单调递增,
故函数f(x)=x+1没有峰值.
(2)函数f(x)=x2+4x+1=(x+2)2-3,结合二次函数图象可知:
当x<-2时,函数图形递减;当-2<x时,函数图象递增.
故f(-2)为函数f(x)=x2+4x+1的峰值,
f(-2)=(-2+2)2-3=3,
答:函数f(x)=x2+4x+1的峰值为-3.
(3)根据x-1=0、m=0和m2-1=0,将整个x的取值分五段考虑.
①当m<-1时,即m<0,m2-1>0,
此时图象T1单调递增;图象T2单调递增.
故当m<-1时,图象T所对应的函数f(x)无峰值;
②当m=±1时,图象T2为平行x轴的一条射线,即在此区间f(x)为定值,
故当m=±1时,图象T所对应的函数f(x)无峰值;
③当-1<m<0时,即m<0,m2-1<0,
此时图象T1单调递增;图象T2单调递减.
且当x=m时,y=m(m-1)2+2m2=m3+m;y=(m2-1)m+2m=m3+m,即图象T在m处连续.
故当-1<m<0时,函数f(x)存在峰值f(m).
④当0<m<1时,即m>0,m2-1<0,
此时图象T1单调递减;图象T2单调递减.
故当0<m<1时,图象T所对应的函数f(x)无峰值;
⑤当1<m时,结合二次函数y=m(x-1)2+2m2(x≤m)的图象T1可知:
当x<1时,函数f(x)单调递减;当1<x≤m时,函数f(x)单调递增.
即f(1)是函数f(x)的峰值.
故当1<m时,图象T所对应的函数记为f(x)有峰值f(1).
综上可知:若f(x)存在峰值,实数m的取值范围为-1<m<0或1<m.
点评 本题考查了一次函数和二次函数的性质,解题的关键:(1)一次函数具有单调性;(2)熟悉二次函数的性质;(3)分段考虑,并将一次函数与二次函数性质相结合.本题属于中档题,(1)(2)难度不大,(3)具有一定的难度,主要在于将m分类讨论,失分点在于当-1<m<0时,要得出函数图象T在m处连续.

 阅读快车系列答案
阅读快车系列答案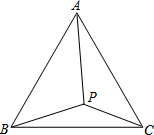 P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?
P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?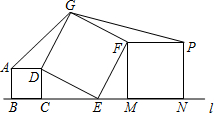 在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.