题目内容
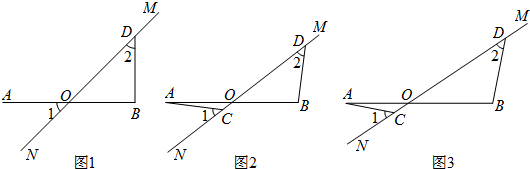
8.如图1,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数y=-x2的图象为C1.(1)平移抛物线C1,使平移后的抛物线经过点A,但不过点B,则向下平移且经过点A的解析式为y=-x2-1
(2)平移抛物线C2,使平移后的抛物线经过A、B两点,所得的抛物线为C3,如图2,求抛物线C3的解析式及在AB上方的抛物线上找一点C,使△ABC的面积最大,并求这个最大面积.
(3)在y轴上是否存在点P,使S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由.

分析 (1)设平移以后的二次函数解析式是:y=-x2+c,把(1,-2)代入即可求得c的值,得到函数的解析式;
(2)利用待定系数法即可求得函数的解析式,根据待定系数法求得AB的解析式,再设过点C与AB平行的直线的解析式,根据△=0求得C点坐标,进一步得到△ABC的面积;
(3)分当点P位于AB的上方和下方两种情况进行讨论求解.
解答 解:(1)设平移以后的二次函数解析式是:y=-x2+c,
把A(1,-2)代入得:-1+c=-2,
解得:c=-1,
则函数的解析式是:y=-x2-1.
故答案为:y=-x2-1;
(2)设C2的解析式是y=-x2+bx+c,
因为C2经过点A(1,-2)和B(3,-1),
根据题意得:$\left\{\begin{array}{l}{-2=-1+b+c}\\{-1=-9+3b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{9}{2}}\\{c=-\frac{11}{2}}\end{array}\right.$,
则C2的解析式是:y=-x2+$\frac{9}{2}$x-$\frac{11}{2}$,
设AB的解析式为y=kx+b,则$\left\{\begin{array}{l}{k+b=-2}\\{3k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-\frac{5}{2}}\end{array}\right.$.
故AB的解析式为y=$\frac{1}{2}$x-$\frac{5}{2}$,
设过点C与AB平行的直线的解析式为y=$\frac{1}{2}$x+m,与C2的解析式y=-x2+$\frac{9}{2}$x-$\frac{11}{2}$联立得-x2+$\frac{9}{2}$x-$\frac{11}{2}$=$\frac{1}{2}$x+m,
即x2-4x+(m+$\frac{11}{2}$)=0,
△=16-4(m+$\frac{11}{2}$)=0,
解得m=-$\frac{3}{2}$,
则x=2,
y=-$\frac{1}{2}$,
即点C的坐标为(2,-$\frac{1}{2}$),
则S△ABC=2×$\frac{3}{2}$-1×$\frac{3}{2}$×$\frac{1}{2}$-1×$\frac{1}{2}$×$\frac{1}{2}$-2×1×$\frac{1}{2}$=1.
(3)AB的解析式为y=$\frac{1}{2}$x-$\frac{5}{2}$,过点C与AB平行的直线的解析式为y=$\frac{1}{2}$x-$\frac{3}{2}$,
①当点P位于AB的上方时,点P的坐标为(0,-$\frac{3}{2}$);
②当点P位于AB的下方时,点P的坐标为(0,-$\frac{5}{2}$×2+$\frac{3}{2}$),即(0,-$\frac{7}{2}$).
综上所述,所求点P的坐标为(0,-$\frac{3}{2}$)或(0,-$\frac{7}{2}$).
点评 本题考查了二次函数综合题,是待定系数法求函数的解析式,以及函数的平移的综合,正确理解平移时,函数解析式的变化规律是关键.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | -$\frac{5}{2}$ |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{6}$ |
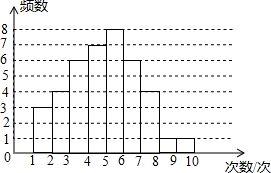 为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.
为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.