题目内容
3．一个袋子中装有大小完全相同的3个乒乓球，其中2个白色，1个黄色．请你用它为甲、乙两位同学设计一个能决定胜负的公平的摸球游戏规则．并说明公平的理由．分析 制定游戏规则关键要看游戏双方取胜的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等即可．
解答 解：游戏规则：从袋子中摸出一个球，记录其颜色，放回，搅匀，再从袋子中摸出一球；若两个都是白色，则甲胜；若两个为一个黄色一个白色，则乙胜，（游戏规则不唯一）
理由如下：
从树形可知，共有9种可能，且都是等可能，其中两个都是白色的有4种可能，一个黄色一个色的有4种可能，
∴P（甲）=P（乙）=$\frac{4}{9}$，
∴游戏公平．
点评 此题考查了游戏的公平性，以及列表法与树状图法，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．
练习册系列答案
53随堂测系列答案
相关题目
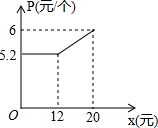某企业接到一批零件的加工任务，要求在20天内完成，这批零件的出厂价为每个6元．为按时完成任务，该企业招收了新工人，在6天的培训期内，新工人小亮第x天能加工80x个零件，培训后小亮第x天内加工的零件个数为（50x+200）个．