题目内容
16.九(3)班“2016年新年联欢会”中,有一个摸奖游戏,规则如下:有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸.现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.(1)现小芳有一次翻牌机会,若正面是笑脸的就获奖,正面是哭脸的不获奖.她从中随机翻开一张纸牌,则小芳获奖的概率是$\frac{1}{2}$;
(2)如果小芳、小明都有翻两张牌的机会.小芳先翻一张,放回洗匀后再翻一张;小明同时翻开两张纸牌.他们各自翻开的两张纸牌中只要出现笑脸就获奖.他们获奖的机会相等吗?分析说明理由.
分析 (1)根据正面有2张笑脸、2张哭脸,直接利用概率公式求解即可求得答案;
(2)首先根据题意分别列出表格,然后由表格即可求得所有等可能的结果与获奖的情况,再利用概率公式求解即可求得他们获奖的概率,比较即可求得答案.
解答 解:(1)∵有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸,翻一次牌正面是笑脸的就获奖,正面是哭脸的不获奖,
∴获奖的概率是 $\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)他们获奖机会不相等,理由如下:
小芳:
第一张 第二张 | 笑1 | 笑2 | 哭1 | 哭2 |
| 笑1 | 笑1,笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 |
| 笑2 | 笑1,笑2 | 笑2,笑2 | 哭1,笑2 | 哭2,笑2 |
| 哭1 | 笑1,哭1 | 笑2,哭1 | 哭1,哭1 | 哭2,哭1 |
| 哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 | 哭2,哭2 |
∴P(小芳获奖)=$\frac{12}{16}$=$\frac{3}{4}$;
小明:
第一张 第二张 | 笑1 | 笑2 | 哭1 | 哭2 |
| 笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 | |
| 笑2 | 笑1,笑2 | 哭1,笑2 | 哭2,笑2 | |
| 哭1 | 笑1,哭1 | 笑2,哭1 | 哭2,哭1 | |
| 哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 |
∴P(小明获奖)=$\frac{10}{12}$=$\frac{5}{6}$,
∵P(小芳获奖)≠P(小明获奖),
∴他们获奖的机会不相等.
点评 此题考查了列表法或树状图法求概率.注意小芳属于放回实验,小明属于不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
1.在实数$\sqrt{4}$、$\sqrt{3}$、$\frac{1}{3}$、0.$\stackrel{•}{3}$、π、2.1234567891011121314…(自然数依次排列)、$\root{3}{-8}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.太阳的半径为696000千米,把696000这个数据用科学记数法表示为( )
| A. | 696×103 | B. | 69.6×104 | C. | 6.96×105 | D. | 6.96×106 |
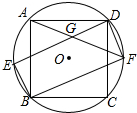 正方形ABCD内接于⊙O,如图所示,在劣弧$\widehat{AB}$上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
正方形ABCD内接于⊙O,如图所示,在劣弧$\widehat{AB}$上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: 如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是$\frac{1}{3}$.
如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是$\frac{1}{3}$.