题目内容
16．因式分解：$\frac{1}{3}{a}^{3}$-3a=$\frac{1}{3}$a（a+3）（a-3）．分析 原式提取公因式，再利用平方差公式分解即可．
解答 解：原式=$\frac{1}{3}$a（a2-1）
=$\frac{1}{3}$a（a+3）（a-3）．
故答案为：$\frac{1}{3}$a（a+3）（a-3）．
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
6．
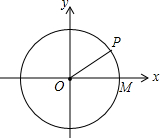在平面直角坐标系中，以原点O为圆心的⊙O交x轴正半轴为M，P为圆上一点，坐标为（$\sqrt{3}$，1），则cos∠POM=（ ）
在平面直角坐标系中，以原点O为圆心的⊙O交x轴正半轴为M，P为圆上一点，坐标为（$\sqrt{3}$，1），则cos∠POM=（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |
7．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | （3a）3=9a3 | C． | a3-2a3=-1 | D． | （a2）3=a6 |
11．下列计算正确的是（ ）
| A． | b3•b4=b7 | B． | （b3）4=b7 | C． | b3+b4=b7 | D． | b6÷b3=b2 |
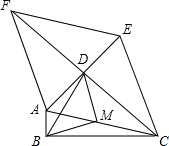定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个矩形的直径．如图，△ABC中．∠ABC=90°，以AC为一边向形外作菱形ACEF，点D是菱形ACEF对角线的交点，可以得到损矩形ABCD，连接BD，则有∠DBC=∠DAC，∠DBC=60°，∠ACB=15°
如图，已知AB∥CD，∠BAE=3∠ECF，∠ECF=28°，求∠E的度数．