题目内容
2. 如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.
如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.
分析 利用面积的和差分别计算出甲图中阴影部分的面积=a2-b2,乙图中阴影部分的面积=a2-ab,则根据分式的运算可得到m=1+$\frac{b}{a}$,然后根据a>b>0可确定m的取值范围.
解答 解:甲图中阴影部分的面积=a2-b2,乙图中阴影部分的面积=a2-ab,
所以m=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$=$\frac{(a+b)(a-b)}{a(a-b)}$=$\frac{a+b}{a}$=1+$\frac{b}{a}$,
而a>b>0,
所以1<m<2.
故答案为1<m<2.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.注意代数式的书写形式.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
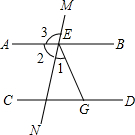 如图,AB∥CD,∠1:∠2:∠3=1:4:5
如图,AB∥CD,∠1:∠2:∠3=1:4:5 如图,△ABC中,D、E分别是AB、AC的中点,连结DE、BE、DC,且BE和DC交于点O,S△DEO=1,则S△OBC=( )
如图,△ABC中,D、E分别是AB、AC的中点,连结DE、BE、DC,且BE和DC交于点O,S△DEO=1,则S△OBC=( )