题目内容
12．（1）如果三角形三个内角度数的比为1：2：3，试判断三角形的形状并说明理由；（2）如果四边形各内角度数的比为1：2：3：4，求四个内角的度数；
（3）五边形五个内角度数的比能否是1：2：3：4：5？若能，请求出各角度数；若不能，请说明理由．
分析 （1）根据三角形内角和等于180°列方程解答即可；
（2）根据四边形内角和等于360°列方程解答即可；
（3）根据五边形内角和等于540°列方程解答即可．
解答 解：（1）设三个内角度数分别为x、2x、3x，
则x+2x+3x=180°，
解得，x=30°，
则2x=60°、3x=90°，
这个三角形是直角三角形；
（2）设四个内角度数分别为x、2x、3x、4x，
则x+2x+3x+4x=360°，
解得x=36°，
则2x=72°、3x=108°、4x=144°；
（3）设五个内角度数分别为x、2x、3x、4x、5x，
则x+2x+3x+4x+5x=540°，
解得x=36°，
则2x=72°、3x=108°、4x=144°、5x=180°，
∵五边形的内角度数不可能是180°，
∴五边形五个内角度数的比不能是1：2：3：4：5．
点评 本题考查的是多边形的内角和定理的应用，掌握n边形内角和公式（n-2）×180°是解题的关键．
练习册系列答案
相关题目
如图，在?ABCD中，E、F在平行四边形的外部，且AE=CF，BE=DF，试指出AC和EF的关系，并说明理由．
4．下个各式成立的是（ ）
| A． | $\sqrt{（-2）^{2}}$=-2 | B． | $\sqrt{（-5）^{2}}$=-5 | C． | $\sqrt{（-6）^{2}}$=6 | D． | $\sqrt{{x}^{2}}$=x |
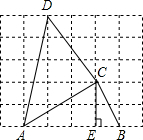如图，在方格纸上的每个小正方形的边长都是1，点A，B，C，D都在正方形的顶点上．
如图，设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$（a＞b＞0），则m的取值范围是1＜m＜2．