题目内容
13．已知关于x、y的方程组$\left\{\begin{array}{l}{2x+y=1+4m}\\{x+2y=2-m}\end{array}\right.$的解满足x+y＜0，则m的取值范围是m＜-1．分析 方程组两方程相加表示出x+y，代入已知不等式求出m的范围即可．
解答 解：$\left\{\begin{array}{l}{2x+y=1+4m①}\\{x+2y=2-m②}\end{array}\right.$，
①+②得：3（x+y）=3+3m，即x+y=1+m，
代入得：1+m＜0，
解得：m＜-1，
故答案为：m＜-1
点评 此题考查了二元一次方程组的解，熟练掌握运算法则是解本题的关键．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
4．下个各式成立的是（ ）
| A． | $\sqrt{（-2）^{2}}$=-2 | B． | $\sqrt{（-5）^{2}}$=-5 | C． | $\sqrt{（-6）^{2}}$=6 | D． | $\sqrt{{x}^{2}}$=x |
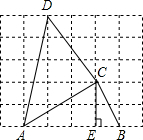如图，在方格纸上的每个小正方形的边长都是1，点A，B，C，D都在正方形的顶点上．
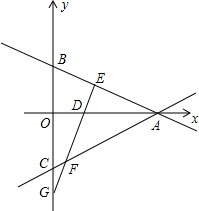如图，在平面直角坐标系中，一直线分别与坐标轴交于A（a，0）、B（0，b）两点，满足$\sqrt{（a-3）^{2}}$+|b-1|=0，在y轴负半轴上截取OC=OB．
在△ABC中，∠B=∠C，点D、E分别在BC、AC上，AD=AE，试猜想∠BAD和∠EDC有何数量关系？并说明理由．
如图，设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$（a＞b＞0），则m的取值范围是1＜m＜2．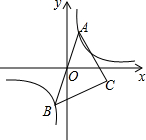
如图，已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=$\frac{k}{x}$（k＜0）上运动，则k的值是-1．