题目内容
10.在直角坐标系中,A(1,1),B(5,1),C(6,3),D(2,3),顺次连接A,B,C,D,则四边形ABCD的形状是平行四边形,对角线交点O的坐标是($\frac{7}{2}$,2).分析 由A、B、C、D的坐标得出四边形ABCD是平行四边形,由平行四边形的对角线互相平分得出O是AC的中点,即可得出点O的坐标.
解答 解:如图所示: ∵A(1,1),B(5,1),C(6,3),D(2,3),
∵A(1,1),B(5,1),C(6,3),D(2,3),
∴AB∥CD,AB=5-1=4,CD=6-2=4,
∴AB=CD,
∴四边形ABCD是平行四边形;
∴AC与BD互相平分,
即O为AC的中点,
∴点O的横坐标为:$\frac{1+6}{2}$=$\frac{7}{2}$,
点O的纵坐标为:$\frac{1+3}{2}$=2,
∴点O的坐标为($\frac{7}{2}$,2);
故答案为:平行四边形,($\frac{7}{2}$,2).
点评 本题考查了平行四边形的判定与性质、坐标与图形性质;熟练掌握平行四边形的判定与性质并能进行推理计算是解决问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
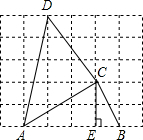 如图,在方格纸上的每个小正方形的边长都是1,点A,B,C,D都在正方形的顶点上.
如图,在方格纸上的每个小正方形的边长都是1,点A,B,C,D都在正方形的顶点上. 在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由.
在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由. 如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.
如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.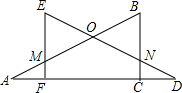 两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.
两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.