题目内容
17.已知关于x,y的方程满足方程组$\left\{\begin{array}{l}{3x+2y=m+1}\\{2x+y=m-1}\end{array}\right.$.(1)若x-y=2,求m的值;
(2)若x,y,m均为非负数,求m的取值范围,并化简式子|m-3|+|m-5|;
(3)在(2)的条件下求s=2x-3y+m的最小值及最大值.
分析 (1)把m看做已知数表示出方程组的解,得到x与y,代入x-y=2求出m的值即可;
(2)根据x,y为非负数求出m的范围,判断出绝对值里边式子的正负,利用绝对值的代数意义化简,计算即可得到结果;
(3)把表示出的x与y代入s,利用一次函数性质求出最大值与最小值即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+2y=m+1①}\\{2x+y=m-1②}\end{array}\right.$,
①-②×2得:-x=-m+3,即x=m-3,
把x=m-3代入②得:2m-6+y=m-1,即y=-m+5,
把x=m-3,y=-m+5代入x-y=2中,得:m-3+m-5=2,即m=5;
(2)由题意得:$\left\{\begin{array}{l}{m-3≥0}\\{-m+5≥0}\end{array}\right.$,
解得:3≤m≤5,
∴m-3≥0,m-5≤0,
则原式=m-3+5-m=2;
(3)根据题意得:s=2m-6+3m-15+m=6m-21,
∵3≤m≤5,
∴当m=3时,s=-3;m=5时,s=9,
则s的最小值为-3,最大值为9.
点评 此题考查了二元一次方程组的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角之比为1:2:3 | B. | 三边平方的比为1:2:3 | ||
| C. | 三边长为41,40,9 | D. | 三边长为10,15,20 |
 如图,在?ABCD中,E、F在平行四边形的外部,且AE=CF,BE=DF,试指出AC和EF的关系,并说明理由.
如图,在?ABCD中,E、F在平行四边形的外部,且AE=CF,BE=DF,试指出AC和EF的关系,并说明理由.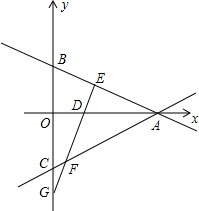 如图,在平面直角坐标系中,一直线分别与坐标轴交于A(a,0)、B(0,b)两点,满足$\sqrt{(a-3)^{2}}$+|b-1|=0,在y轴负半轴上截取OC=OB.
如图,在平面直角坐标系中,一直线分别与坐标轴交于A(a,0)、B(0,b)两点,满足$\sqrt{(a-3)^{2}}$+|b-1|=0,在y轴负半轴上截取OC=OB. 在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由.
在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由. 如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.
如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.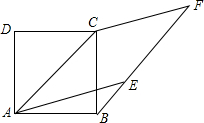 如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.
如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.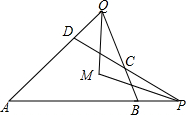 如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.
如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.