题目内容
14.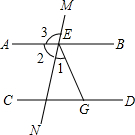 如图,AB∥CD,∠1:∠2:∠3=1:4:5
如图,AB∥CD,∠1:∠2:∠3=1:4:5(1)求∠3的度数;
(2)射线EB是∠MEG的平分线吗?为什么?
分析 (1)由∠1:∠2:∠3=1:4:5,设∠1=x,∠2=4x,∠3=5x,由∠2+∠3=180°,得到4x+5x=180°,解得:x=20°,所以∠3=5×20°=100°.
(2)射线EB是∠MEG的平分线,利用平角分别求出∠MEB=180°-∠3=180°-100°=80°,∠BEG=180°-∠1-∠2=180°-20°-80°=80°,得到∠BEG=∠MEB,射线EB是∠MEG的平分线.
解答 解:(1)由∠1:∠2:∠3=1:4:5,设∠1=x,∠2=4x,∠3=5x,
∵∠2+∠3=180°,
∴4x+5x=180°,
解得:x=20°,
∴∠3=5×20°=100°.
∠1=20°,∠2=80°.
(2)射线EB是∠MEG的平分线,
∵∠3=100°,
∴∠MEB=180°-∠3=180°-100°=80°,
∵∠1+∠2+∠BEG=180°,
∴∠BEG=180°-∠1-∠2=180°-20°-80°=80°,
∴∠BEG=∠MEB,
∴射线EB是∠MEG的平分线.
点评 本题考查了角的计算,解决本题的关键是由∠1:∠2:∠3=1:4:5,设∠1=x,∠2=4x,∠3=5x,利用平角分别求出∠1,∠2,∠3的度数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下个各式成立的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{(-5)^{2}}$=-5 | C. | $\sqrt{(-6)^{2}}$=6 | D. | $\sqrt{{x}^{2}}$=x |
 在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由.
在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由. 如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.
如图,设m=$\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$(a>b>0),则m的取值范围是1<m<2.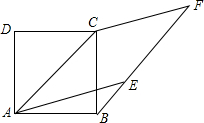 如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.
如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.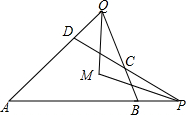 如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.
如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.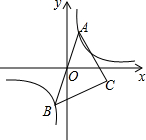 如图,已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-1.
如图,已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-1.