题目内容
3.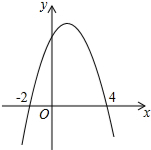 如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).
如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).(1)求此二次函数的顶点坐标;
(2)根据函数的图象,直接写出当函数值y>0时,自变量x的取值范围.
分析 (1)把抛物线的解析式化为顶点式即可求出其顶点坐标;
(2)当y>0时,即抛物线在x轴的上方的部分,写出对应的x的取值范围即可.
解答 解:(1)∵y=-x2+2x+8=-(x-1)2+9,
∴顶点坐标为(1,9);
(2)由函数图象可知当y>0时,即抛物线在x轴的上方的部分,此时对应自变量x的取值范围是-2<x<4.
点评 本题考查了抛物线与x轴的交点的问题以及借组与函数的图形求自变量取值范围,能够结合函数图象正确的判定自变量的取值范围是解题关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
12. 将一副三角尺按如图方式进行摆放,则∠1的度数为( )
将一副三角尺按如图方式进行摆放,则∠1的度数为( )
 将一副三角尺按如图方式进行摆放,则∠1的度数为( )
将一副三角尺按如图方式进行摆放,则∠1的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 135° |
13. 二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
 二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3. 观察如图,A点为正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象的交点
观察如图,A点为正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象的交点 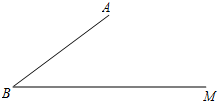 如图,已知cos∠ABM=$\frac{4}{5}$,AB=20,C是射线BM上一点.
如图,已知cos∠ABM=$\frac{4}{5}$,AB=20,C是射线BM上一点.