题目内容
13. 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)用配方法将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)当x取何值时,y随x的增大而减少?
(4)当-2<x<3时,观察图象直接写出函数y的取值范围.
分析 (1)由于二次项系数是1,利用配方法直接加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)根据二次函数的性质画出图象即可;
(3)根据二次函数的增减性即可求解;
(4)观察图象即可求解.
解答 解:(1)y=x2-2x-3=x2-2x+1-4=(x-1)2-4,
即y=(x-1)2-4;
(2)∵二次函数y=x2-2x-3的开口向上,对称轴为直线x=1,
顶点坐标为(1,-4),与x轴的交点为(3,0),(-1,0),与y轴的交点为(0,-3),
∴其图象为:
(3)∵二次函数y=x2-2x-3的开口向上,对称轴为直线x=1,
∴当x≤1时,y随x的增大而减少;
(4)观察图象可得,当-2<x<3时,函数y的取值范围是-4≤y<5.
点评 本题考查了二次函数的三种形式,二次函数的图象与性质及用描点法画二次函数的图象,利用数形结合是解此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.已知直线上有A,B,C三个点,其中AB=4,BC=3,则AC=( )
| A. | 2 | B. | 7 | C. | 2或7 | D. | 1或7 |
18.下列关系式中,属于二次函数的是(x为自变量)( )
| A. | y=$\frac{1}{8}{x^2}$ | B. | y=$\sqrt{{x^2}-1}$ | C. | y=$\frac{1}{x^2}$ | D. | y=$\frac{1}{x}$ |
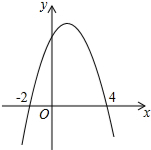 如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).
如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).