题目内容
14. 观察如图,A点为正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象的交点
观察如图,A点为正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象的交点 (1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧)分别交y=$\frac{3}{4}$x和y=-x+7的图象于点B,C,连接OC,若BC=$\frac{14}{5}$OA,求△OBC的面枳.
分析 (1)联立两一次函数的解析式求出x、y的值即可得出A点坐标;
(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中根据勾股定理求出OA的长,故可得出BC的长,根据P(a,0)可用a表示出B、C的坐标,故可得出a的值,由三角形的面积公式即可得出结论.
解答 解:(1)由题意得$\left\{\begin{array}{l}{y=\frac{3}{4}x}\\{y=-x+7}\end{array}\right.$,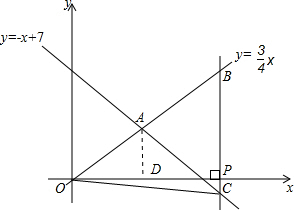
解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$.
则A(4,3);
(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理得,
OA=$\sqrt{O{D}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
∴BC=$\frac{14}{5}$OA=$\frac{14}{5}$×5=14.
∵P(a,0),
∴B(a,$\frac{3}{4}$a),C(a,-a+7),
∴BC=$\frac{3}{4}$a-(-a+7)=$\frac{7}{4}$a-7,
∴$\frac{7}{4}$a-7=14,解得a=12,
∴S△OBC=$\frac{1}{2}$BC•OP=$\frac{1}{2}$×14×12=84.
点评 本题考查的是两条直线相交或平行问题,根据题意作出辅助线.构造出直角三角形是解答此题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
9.下列运算正确的是( )
| A. | 3x5-4x3=-x2 | B. | 2$\sqrt{3}+2\sqrt{2}=2\sqrt{5}$ | ||
| C. | (-x)4•(-x2)=-x8 | D. | (3a5x3-9ax5)÷(-3ax3)=3x2-a4 |
19. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )| A. | (33,32) | B. | (31,32) | C. | (33,16) | D. | (31,16) |
6.利用一副三角尺不能画出的角的度数是( )
| A. | 15° | B. | 80° | C. | 105° | D. | 135° |
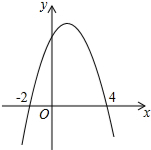 如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).
如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0). 如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.