题目内容
11.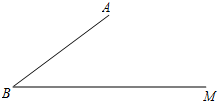 如图,已知cos∠ABM=$\frac{4}{5}$,AB=20,C是射线BM上一点.
如图,已知cos∠ABM=$\frac{4}{5}$,AB=20,C是射线BM上一点.(1)求点A到BM的距离;
(2)在下列条件中,可以唯一确定BC长的是②③(填写所有符合条件的序号),
①AC=13;②tan∠ACB=$\frac{12}{5}$; ③连接AC,△ABC的面积为126.
分析 (1)过A作AH⊥BC于H,利用余弦定义可计算出BH=16,在利用勾股定理可计算出AH=12,
(2)由于以A为圆心,13为半径作圆与BM有两个交点,即此时C点有两个,BC的长不确定;若tan∠ACB=$\frac{12}{5}$,在Rt△ACH中利用正切的定义可求出CH=5,所以BC=BH+CH=21;若当△ABC的面积为126时,则可利用三角形面积公式求出BC的长,于是得到符合条件的序号.
解答 解:(1)过A作AH⊥BC于H,
∵cos∠ABM=$\frac{BH}{AB}$=$\frac{4}{5}$,
∴BH=$\frac{4}{5}$×20=16,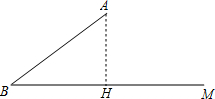
∴AH=$\sqrt{2{0}^{2}-1{6}^{2}}$=12,
即点A到BM的距离为12;
(2)当AC=13时,以A为圆心,13为半径作圆与BM有两个交点,所以此时C点有两个;
当tan∠ACB=$\frac{12}{5}$,在Rt△ACH中,tan∠ACH=$\frac{AH}{CH}$=$\frac{12}{5}$,则CH=5,所以BC=BH+CH=16+5=21;
当△ABC的面积为126时,则$\frac{1}{2}$•12•BC=216,所以BC=36.
故答案为②③.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活运用勾股定理和锐角三角函数的定义.

练习册系列答案
相关题目
19. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),则B5的坐标是( )| A. | (33,32) | B. | (31,32) | C. | (33,16) | D. | (31,16) |
6.利用一副三角尺不能画出的角的度数是( )
| A. | 15° | B. | 80° | C. | 105° | D. | 135° |
16.不等式2x+2<6的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
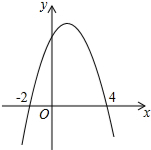 如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).
如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).