题目内容
18.已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).(1)求此二次函数的表达式,并用配方法将其化为y=a(x-h)2+k的形式;
(2)画出此函数图象的示意图.
分析 (1)先将点(-1,-8),(0,-3)代入y=-x2+bx+c,列出关于b、c的二元一次方程组,求解得出b、c的值,得到二次函数的表达式,再用配方法化为顶点式的形式
(2)利用描点法画出函数图象即可.
解答 解:(1)∵二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3),
∴$\left\{\begin{array}{l}{-1-b+c=-8}\\{c=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=4}\\{c=-3}\end{array}\right.$,
∴此二次函数的表达式为y=-x2+4x-3;
y=-x2+4x-3=-(x-2)2+1;
(2)∵y=-(x-2)2+1,
∴顶点坐标为(2,1),对称轴方程为x=2.
∵函数二次函数y=-x2+4x-3的开口向下,顶点坐标为(2,1),与x轴的交点为(3,0),(1,0),
∴其图象为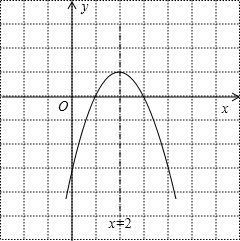
点评 本题考查的是待定系数法求二次函数的解析式,二次函数的三种形式,二次函数的性质及用描点法画二次函数的图象,能利用待定系数法求出二次函数的解析式是解答此题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
9.下列运算正确的是( )
| A. | 3x5-4x3=-x2 | B. | 2$\sqrt{3}+2\sqrt{2}=2\sqrt{5}$ | ||
| C. | (-x)4•(-x2)=-x8 | D. | (3a5x3-9ax5)÷(-3ax3)=3x2-a4 |
6.利用一副三角尺不能画出的角的度数是( )
| A. | 15° | B. | 80° | C. | 105° | D. | 135° |
7.某种流感病毒的直径在0.00 000 012米左右,将0.00 000 012用科学记数法表示应为( )
| A. | 0.12×10-6 | B. | 12×10-8 | C. | 1.2×10-6 | D. | 1.2×10-7 |

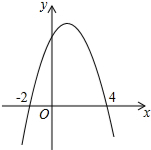 如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0).
如图,二次函数y=-x2+2x+8图象与x轴的交点坐标为(-2,0),(4,0). 如图,正方形网格中每个小正方形边长都是l,则△ABC的外接圆的圆心坐标为(8.5,2).
如图,正方形网格中每个小正方形边长都是l,则△ABC的外接圆的圆心坐标为(8.5,2).