Question

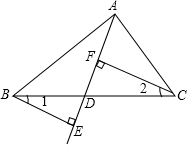
1．完成下列的证明：
已知，如图，D是BC上任意一点，BE⊥AD，交AD的延长线于点E，CF⊥AD，垂足为F，求证：∠1=∠2．
证明：∵BE⊥AD
∴∠BED=90°（垂直的定理）
又∵CF⊥AD
∴∠CFD=90°
∴∠BED=∠CFD
∴BE∥CF（内错角相等，两直线平行）
∴∠1=∠2（两直线平行，内错角相等）

Answer 1

分析 根据平行的判定定理以及平行线的性质定理即可解答．

解答 证明：∵BE⊥AD
∴∠BED=90°（垂直的定义）
又∵CF⊥AD
∴∠CFD=90°，
∴∠BED=∠CFD，
∴BE∥CF（内错角相等，两直线平行）
∴∠1=∠2（两直线平行，内错角相等 ）．

点评 本题考查了平行线的判定定理和性质定理，正确理解定理的内容是关键．