题目内容
13.已知AB与DE,AC与DF对应,且AB=4cm,BC=5cm,AC=8cm,DE=1$\frac{2}{3}$cm,DF=3$\frac{1}{3}$cm,则EF=$\frac{25}{12}$时,△ABC∽△DEF.分析 若△ABC∽△DEF,则有$\frac{AB}{DE}=\frac{BC}{EF}$,代入可求得EF.
解答 解:若△ABC∽△DEF,则有$\frac{AB}{DE}=\frac{BC}{EF}$,
因为AB=4,BC=5,DE=1$\frac{2}{3}$,
所以$\frac{4}{5}=\frac{1\frac{2}{3}}{EF}$,
解得EF=$\frac{25}{12}$,
即当EF=$\frac{25}{12}$时,△ABC∽△DEF.
故答案为:$\frac{25}{12}$.
点评 本题主要考查相似三角形的性质,由三角形相似得到对应边的比相等是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
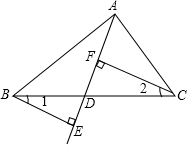 完成下列的证明:
完成下列的证明: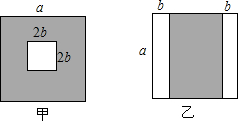 如图,有甲、乙两种边长为a的正方形印花砖,阴影部分代表印花区域,空白部分代表留白区域,甲的留白区域是正方形,乙的留白区域是两个长方形.
如图,有甲、乙两种边长为a的正方形印花砖,阴影部分代表印花区域,空白部分代表留白区域,甲的留白区域是正方形,乙的留白区域是两个长方形. 若a、b、c三数在数轴上对应位置如图所示,化简|a|-|a+b|+|c-b|+|a+c|.
若a、b、c三数在数轴上对应位置如图所示,化简|a|-|a+b|+|c-b|+|a+c|.