题目内容
10.解不等式:(1)x+12≥2x-$\frac{1}{3}$;
(2)1-$\frac{2x}{3}$>-2;
(3)5x+4<2x+10.
分析 (1)先移项得到x-2x≥-$\frac{1}{3}$-12,然后合并后把x的系数化为1即可;
(2)先移项,然后合并后把x的系数化为1即可;
(2)先移项后合并,然后合并后把x的系数化为1即可.
解答 解:(1)移项得x-2x≥-$\frac{1}{3}$-12,
合并得-x≥-$\frac{37}{3}$,
系数化为1得x≤$\frac{37}{3}$;
(2)移项得-$\frac{2}{3}$x>-2-1,
即-$\frac{2}{3}$x>-3,
系数化为1得x<$\frac{9}{2}$;
(3)移项得5x-2x<10-4,
合并得3x<6,
系数化为1得x<2.
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.

练习册系列答案
相关题目
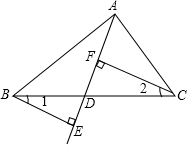 完成下列的证明:
完成下列的证明: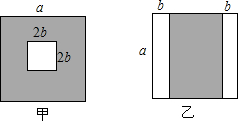 如图,有甲、乙两种边长为a的正方形印花砖,阴影部分代表印花区域,空白部分代表留白区域,甲的留白区域是正方形,乙的留白区域是两个长方形.
如图,有甲、乙两种边长为a的正方形印花砖,阴影部分代表印花区域,空白部分代表留白区域,甲的留白区域是正方形,乙的留白区域是两个长方形.