题目内容
7．先化简再求值：$\frac{x-3}{x-2}$÷（x+2-$\frac{5}{x-2}$），其中x是方程x2-7x+10=0的根．分析 先根据分式混合运算的法则把原式进行化简，再求出x的值代入进行计算即可．
解答 解：原式=$\frac{x-3}{x-2}$÷$\frac{{x}^{2}-9}{x-2}$
=$\frac{x-3}{x-2}$•$\frac{x-2}{（x+3）（x-3）}$
=$\frac{1}{x+3}$，
解方程x2-7x+10=0得，x1=2，x2=5，
当x=2时，原分式无意义；
当x=5时，原式=$\frac{1}{5+3}$=$\frac{1}{8}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
18．下列运算正确的是（ ）
| A． | 3m4÷m3=3m2 | B． | m+m2=m3 | C． | （m+n）（m-n）=m2-n2 | D． | （$\frac{m}{2}$）3=$\frac{{m}^{3}}{2}$ |
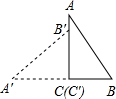如图，将一块斜边长为15cm，∠B=60°的直角三角板ABC，绕点C逆时针方向旋转90°至△A′B′C′的位置，再沿B′刚好落在斜边AB上，则此三角板向右平移的距离为$\frac{15}{2}$-$\frac{15\sqrt{3}}{2}$．