题目内容
12.等腰△ABC中,AB=AC=4,高BD=2$\sqrt{3}$,则BC=4.分析 首先利用勾股定理求出CD的长,进而求出BC的长.
解答 解:设CD=x,则AD=4-x,
在Rt△BDC和Rt△BDA中
∵BD2+AD2=AB2,BD2+CD2=BC2,
∴$\sqrt{B{D}^{2}+A{D}^{2}}$=AB,
即$\sqrt{(2\sqrt{3})^{2}+(4-x)^{2}}$=4
解得:x1=6(不合题意舍去),x2=2,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4.
故答案为4.
点评 此题主要考查了勾股定理以及等腰三角形的性质,得出DC的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.今年3月5日,李克强总理在《政府工作报告》中指出,到2020年,我国经济总量将超过90万亿元,90万亿元用科学记数法表示为( )
| A. | 9×1011元 | B. | 90×1010元 | C. | 9×1012元 | D. | 9×1013元 |
4.由中国发起创立的“亚洲基础设施投资银行”的法定资本金为100 000 000 000美元,用科学记数法表示为( )
| A. | 1.0×109美元 | B. | 1.0×1010美元 | C. | 1.0×1011美元 | D. | 1.0×1012美元 |
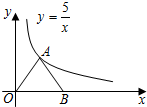 已知反比例函数$y=\frac{5}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=5.
已知反比例函数$y=\frac{5}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=5.