题目内容
17．把一根长为2m的铅丝折成一个矩形，则这个矩形的对角线的长的最小值为$\frac{\sqrt{2}}{2}$m．分析 设矩形的长为xm，宽为（1-x）m，对角线为y，构建二次函数解决问题．
解答 解：设矩形的长为xm，宽为（1-x）m，对角线为y，
则y=$\sqrt{{x}^{2}+（1-x）^{2}}$=$\sqrt{2（x-\frac{1}{2}）^{2}+\frac{1}{2}}$，
∴x=$\frac{1}{2}$时，y的最小值=$\frac{\sqrt{2}}{2}$．
故答案为$\frac{\sqrt{2}}{2}$．
点评 本题考查二次函数的最值问题，解题的关键是构建二次函数，利用二次函数的最值问题解决，属于中考常考题型．
练习册系列答案
相关题目
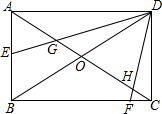已知：如图，在矩形ABCD中，∠EDF两边分别与边AB、BC交于E、F，与对角线交于G、H，且∠EDF=∠BDC，∠BDC=60°，AE=2，DH=$\sqrt{13}$时，DG=$\frac{4\sqrt{13}}{3}$．