题目内容
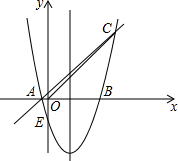 如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).
如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).(1)求直线AC及抛物线的解析式;
(2)连接OC、CB,若点P在抛物线上,且S△POE=
| 1 |
| 2 |
(3)若点Q是线段AC上的动点,作QF⊥x轴交抛物线于F,求线段QF长度的最大值.
考点:二次函数综合题
专题:
分析:(1)由抛物线y=x2+bx+c的对称轴为x=1,可得b=-2,把B(3,0)代入y=x2-2x+c,得c=-3,即可得出抛物线的解析式,把C(4,m)代入y=x2-2x-3,得m=5,由A,C点的坐标,得出AC的解析式为y=x+1,
(2)先由点B,点C的坐标求出S△BOC的值,再由S△POE=
S△BOC求出S△POE的值,设P(t,t2-2t-3),求出t的值即可求出点P的坐标.
(3)设Q(a,a+1),F(a,a2-2a-3),可得|QF|=a+1-(a2-2a-3)=-(a-
)2+
,即可求出线段QF长度的最大值为
.
(2)先由点B,点C的坐标求出S△BOC的值,再由S△POE=
| 1 |
| 2 |
(3)设Q(a,a+1),F(a,a2-2a-3),可得|QF|=a+1-(a2-2a-3)=-(a-
| 3 |
| 2 |
| 25 |
| 4 |
| 25 |
| 4 |
解答:解:(1)∵抛物线y=x2+bx+c的对称轴为x=1,
∴-
=-
=1,
∴b=-2,
∵抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),
∴把B(3,0)代入y=x2-2x+c,得c=-3,
∴抛物线的解析式为y=x2-2x-3,
令0=x2-2x-3得x1=-1,x2=3,
∴A(-1,0),
把C(4,m)代入y=x2-2x-3,得m=5,
∴C(4,5),
设直线AC的解析式为y=kx+b,把A(-1,0),C(4,5)代入,得AC的解析式为y=x+1,
(2)S△BOC=
×3×5=
,
∴S△PDE=
S△BOC=
∵E(0,3),
设P(t,t2-2t-3),
∴S△PDE=
×3×|t|=
,
|t|=
,
P1=(
,-
),P2(-
,
),
(3)设Q(a,a+1),
∴F(a,a2-2a-3)
∴|QF|=a+1-(a2-2a-3)=-a2+3a+4=-(a-
)2+
∴线段QF长度的最大值为
.
∴-
| b |
| 2a |
| b |
| 2 |
∴b=-2,
∵抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),
∴把B(3,0)代入y=x2-2x+c,得c=-3,
∴抛物线的解析式为y=x2-2x-3,
令0=x2-2x-3得x1=-1,x2=3,
∴A(-1,0),
把C(4,m)代入y=x2-2x-3,得m=5,
∴C(4,5),
设直线AC的解析式为y=kx+b,把A(-1,0),C(4,5)代入,得AC的解析式为y=x+1,
(2)S△BOC=
| 1 |
| 2 |
| 15 |
| 2 |
∴S△PDE=
| 1 |
| 2 |
| 15 |
| 4 |
∵E(0,3),
设P(t,t2-2t-3),
∴S△PDE=
| 1 |
| 2 |
| 15 |
| 4 |
|t|=
| 5 |
| 2 |
P1=(
| 5 |
| 2 |
| 7 |
| 4 |
| 5 |
| 2 |
| 33 |
| 4 |
(3)设Q(a,a+1),
∴F(a,a2-2a-3)
∴|QF|=a+1-(a2-2a-3)=-a2+3a+4=-(a-
| 3 |
| 2 |
| 25 |
| 4 |
∴线段QF长度的最大值为
| 25 |
| 4 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
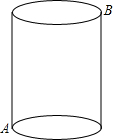 如图,一圆柱体木块高5cm,底面半径
如图,一圆柱体木块高5cm,底面半径

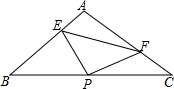 如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.
如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE. 如图,△ABC的内心为I,M、N分别是ABAC的中点,AB>AC,内切圆⊙I与边BC,CA相切于D,E,证明:MN,BI,DE三线共点.
如图,△ABC的内心为I,M、N分别是ABAC的中点,AB>AC,内切圆⊙I与边BC,CA相切于D,E,证明:MN,BI,DE三线共点.