题目内容
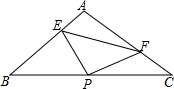 如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.
如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.(1)点A到B C的距离等于
(2)说出△PEF的形状:
(3)用不等式表示EF取值范围:
(4)设FC=x,当x为什么值时,△PCF是等腰三角形?说明理由.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)利用等腰三角形的性质可知AP⊥BC,且可求得AP=
BC,再利用勾股定理求得BC即可求出点A到BC的距离;
(2)连接AP,可证明△APE≌△CFP,从而可判定△PEF的形状;
(3)由(2)可知△PEF为等腰直角三角形,所以EF的长与PE和PF有关,求出PE的取值范围即可得出EF的取值范围;
(4)分CF为底和腰两种情况进行求值即可.
| 1 |
| 2 |
(2)连接AP,可证明△APE≌△CFP,从而可判定△PEF的形状;
(3)由(2)可知△PEF为等腰直角三角形,所以EF的长与PE和PF有关,求出PE的取值范围即可得出EF的取值范围;
(4)分CF为底和腰两种情况进行求值即可.
解答: 解:(1)连接AP,
解:(1)连接AP,
∵AB=AC,P为BC中点,
∴AP⊥BC,
∵AB=AC=2,
∴BC=2
,
∴AP=
BC=
,
即点A到BC的距离为
,
故答案为:
;
(2)∵AB=AC,BE=AF,
∴AE=CF,
由(1)知AP=CP,且AP平分∠BAC,
在△AEP和△CFP中,
,
∴△AEP≌△CFP(SAS),
∴PE=PF,∠APE=∠CPF,
∵∠APF+∠CPF=90°,
∴∠APE+∠APF=90°,
∴△PEF为等腰直角三角形,
故答案为:等腰直角三角形;
(3)∵E点在AB上,
∴当E点在A点或B点时PE最大,此时PE=AP=
,
当E点为AB中点时PE最小,此时PE=
AC=1,
∴1<EF<
,
故答案为:1<EF<
;
(4)当x=1或2时,△PCF为等腰三角形,理由如下:
当△PCF为等腰三角形时,因为∠C=45°,所以只有PF=CF或PC=PF,
当PF=CF时,此时PF⊥CF,可知F为AC中点,所以CF=
AC=1,
当PC=PF时,此时PC⊥PF,即F与点A重合,此时CF=AC=2,
综上可知当x为1或2时△PCF为等腰三角形.
 解:(1)连接AP,
解:(1)连接AP,∵AB=AC,P为BC中点,
∴AP⊥BC,
∵AB=AC=2,
∴BC=2
| 2 |
∴AP=
| 1 |
| 2 |
| 2 |
即点A到BC的距离为
| 2 |
故答案为:
| 2 |
(2)∵AB=AC,BE=AF,
∴AE=CF,
由(1)知AP=CP,且AP平分∠BAC,
在△AEP和△CFP中,
|
∴△AEP≌△CFP(SAS),
∴PE=PF,∠APE=∠CPF,
∵∠APF+∠CPF=90°,
∴∠APE+∠APF=90°,
∴△PEF为等腰直角三角形,
故答案为:等腰直角三角形;
(3)∵E点在AB上,
∴当E点在A点或B点时PE最大,此时PE=AP=
| 2 |
当E点为AB中点时PE最小,此时PE=
| 1 |
| 2 |
∴1<EF<
| 2 |
故答案为:1<EF<
| 2 |
(4)当x=1或2时,△PCF为等腰三角形,理由如下:
当△PCF为等腰三角形时,因为∠C=45°,所以只有PF=CF或PC=PF,
当PF=CF时,此时PF⊥CF,可知F为AC中点,所以CF=
| 1 |
| 2 |
当PC=PF时,此时PC⊥PF,即F与点A重合,此时CF=AC=2,
综上可知当x为1或2时△PCF为等腰三角形.
点评:本题主要考查等腰直角三角形的性质及全等三角形的判定和性质,掌握等腰三角形的性质及全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
若(2x-y)2+2(2x-y)-3=0,则2x-y的值是( )
| A、1或-3 | B、-1或3 |
| C、1 | D、-3 |
已知|a|=5,则|a-2|的值是( )
| A、3 | B、-3或7 |
| C、5或-7 | D、7或3 |
以下各组数为边长的三角形中,能组成直角三角形的是( )
| A、1,2,3 |
| B、2,3,4 |
| C、4,5,6 |
| D、5,12,13 |
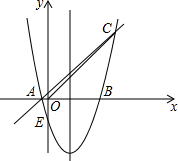 如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).
如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m). 某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.
某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费. 如图,已知△ABC中,AD为BC边上中线,过C任作一条直线交AD于E,交AB于F,求证:AE:ED=2AF:FB.
如图,已知△ABC中,AD为BC边上中线,过C任作一条直线交AD于E,交AB于F,求证:AE:ED=2AF:FB.