题目内容
□ABCD中,点E是BC上的一动点(不与点B、C重合),点F是CD上的一动点(不与点B、C重合).
(1)如图1,若AE=AF,求证:CE=CF.
(2)如图2,若∠BAE=30°,∠DAF=15°,试猜想EF、BE、DF之间的数量关系,并给出证明.
(3)如图3,若∠EAF=45°,连结BD,交AE于M、交AF于N,请探究BM、MN、DN之间的数量关系,并说明理由.

(1)如图1,若AE=AF,求证:CE=CF.
(2)如图2,若∠BAE=30°,∠DAF=15°,试猜想EF、BE、DF之间的数量关系,并给出证明.
(3)如图3,若∠EAF=45°,连结BD,交AE于M、交AF于N,请探究BM、MN、DN之间的数量关系,并说明理由.

考点:四边形综合题
专题:压轴题
分析:(1)根据正方形的四条边都相等可得AB=BC=CD=AD,然后利用“HL”证明Rt△ABE和Rt△ADF全等,根据全等三角形对应边相等可得BE=DF,从而得证;
(2)将△ADF绕点A逆时针旋转90°得到△ABH,根据旋转的性质可得AH=AF,BH=DF,∠BAH=∠DAF,然后求出∠EAH=∠EAF=45°,再利用“边角边”证明△AEF和△AEH全等,根据全等三角形对应边相等可得EH=EF,再根据EH=BE+BH等量代换即可得证;
(3)将△ADN绕点A逆时针旋转90°得到△ABK,根据旋转的性质可得AN=AK,BK=DN,∠BAK=∠DAN,∠ABK=∠ADN=45°,然后求出∠MAN=∠MAK=45°,再利用“边角边”证明△AMN和△AMK全等,根据全等三角形对应边相等可得MN=MK,再求出∠MBK=90°,然后利用勾股定理列式即可.
(2)将△ADF绕点A逆时针旋转90°得到△ABH,根据旋转的性质可得AH=AF,BH=DF,∠BAH=∠DAF,然后求出∠EAH=∠EAF=45°,再利用“边角边”证明△AEF和△AEH全等,根据全等三角形对应边相等可得EH=EF,再根据EH=BE+BH等量代换即可得证;
(3)将△ADN绕点A逆时针旋转90°得到△ABK,根据旋转的性质可得AN=AK,BK=DN,∠BAK=∠DAN,∠ABK=∠ADN=45°,然后求出∠MAN=∠MAK=45°,再利用“边角边”证明△AMN和△AMK全等,根据全等三角形对应边相等可得MN=MK,再求出∠MBK=90°,然后利用勾股定理列式即可.
解答:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴BC-BE=CD-DF,
即CE=CF;

(2)如图,将△ADF绕点A逆时针旋转90°得到△ABH,
由旋转的性质得,AH=AF,BH=DF,∠BAH=∠DAF,
∵∠BAE=30°,∠DAF=15°,
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∵EH=BE+BH,
∴EF=BE+DF;
(3)如图,将△ADN绕点A逆时针旋转90°得到△ABK,
由旋转的性质得,AN=AK,BK=DN,∠BAK=∠DAN,∠ABK=∠ADN=45°,
∵∠EAF=45°,
∴∠MAN=∠MAK=45°,
在△AMN和△AMK中,
,
∴△AMN≌△AMK(SAS),
∴MN=MK,
∵∠MBK=∠ABD+∠ABK=45°+45°=90°,
∴BM2+BK2=MK2,
∴BM2+DN2=MN2.
∴AB=BC=CD=AD,
在Rt△ABE和Rt△ADF中,
|
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴BC-BE=CD-DF,
即CE=CF;

(2)如图,将△ADF绕点A逆时针旋转90°得到△ABH,
由旋转的性质得,AH=AF,BH=DF,∠BAH=∠DAF,
∵∠BAE=30°,∠DAF=15°,
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
|
∴△AEF≌△AEH(SAS),
∴EH=EF,
∵EH=BE+BH,
∴EF=BE+DF;
(3)如图,将△ADN绕点A逆时针旋转90°得到△ABK,
由旋转的性质得,AN=AK,BK=DN,∠BAK=∠DAN,∠ABK=∠ADN=45°,
∵∠EAF=45°,

∴∠MAN=∠MAK=45°,
在△AMN和△AMK中,
|
∴△AMN≌△AMK(SAS),
∴MN=MK,
∵∠MBK=∠ABD+∠ABK=45°+45°=90°,
∴BM2+BK2=MK2,
∴BM2+DN2=MN2.
点评:本题是四边形综合题型,主要利用了正方形的性质,旋转的性质,全等三角形的判定与性质,难点在于利用旋转变换作辅助线构造出全等三角形.

练习册系列答案
相关题目
 如图所示,△ABC,AB=AC,EB=FC,BD=CE,∠A=52°,求∠DEF.
如图所示,△ABC,AB=AC,EB=FC,BD=CE,∠A=52°,求∠DEF. 如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.
如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.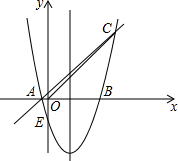 如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).
如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m). 在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C. 如图,如果AB=AC,可补充的条件是
如图,如果AB=AC,可补充的条件是