题目内容
求
+
的最小值．
| x2+9 |
| (4+x)2+25 |
考点：轴对称-最短路线问题
专题：
分析：判断出表示数轴上的点到A（0，3），B（-4，5）的距离最小值，作出图形，找出点A关于x轴的对称点A′，连接A′B，根据轴对称确定最短路线问题，A′B的长度即为最小值，然后利用勾股定理列式计算即可得解．
解答：
解：
+
表示数轴上的点到A（0，3），B（-4，5）的距离最小值，
如图，点A（0，3）关于x轴的对称点A′（0，-3），
连接A′B，则A′B的长度即为最小值，
由勾股定理得，A′B=
=4
，
即
+
的最小值是4
．
解：| x2+9 |
| (4+x)2+25 |
如图，点A（0，3）关于x轴的对称点A′（0，-3），
连接A′B，则A′B的长度即为最小值，
由勾股定理得，A′B=
| 42+82 |
| 5 |
即
| x2+9 |
| (4+x)2+25 |
| 5 |
点评：本题考查了利用轴对称确定最短路线问题，考虑利用几何知识求解是解题的关键，作出图形数形结合更容易理解．
练习册系列答案
53天天练系列答案
相关题目
如图所示，△ABC，AB=AC，EB=FC，BD=CE，∠A=52°，求∠DEF．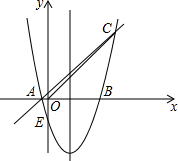
如图，对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B（3，0），另一个交点为A，与y轴交于点E，且经过点C（4，m）．
在平面直角坐标系xOy中，抛物线y=x2-（m-1）x-m（m＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．
某水果种植户去年共摘得一级柑橘4000kg，并计划在今年的某个月内全部售出．由于受季节等因素影响，每千克一级柑橘的月平均售价如图所示（图中各点在同一直线上）．自今年一月份开始，柑橘每多保存一个月将减少200kg，同时需要花费0.02元/kg的保存费．若（2x-y）2+2（2x-y）-3=0，则2x-y的值是（ ）
| A、1或-3 | B、-1或3 |
| C、1 | D、-3 |
