题目内容
 如图,△ABC的内心为I,M、N分别是ABAC的中点,AB>AC,内切圆⊙I与边BC,CA相切于D,E,证明:MN,BI,DE三线共点.
如图,△ABC的内心为I,M、N分别是ABAC的中点,AB>AC,内切圆⊙I与边BC,CA相切于D,E,证明:MN,BI,DE三线共点.考点:圆的综合题,三角形中位线定理,切线长定理,三角形的内切圆与内心
专题:证明题
分析:设MN与BI的延长线的交点为F1,MN与DE的延长线的交点为F2,只需证明F1与F2重合,只需证明MF1=MF2,易证MF1=MB,只需证明MF2=MB,而MF2=MN+NF2,易证NF2=NE,只需证明MB=MN+NE,只需证明MB=MN+NC-EC,只需运用切线长定理就可解决问题.
解答:证明:设MN与BI的延长线的交点为F1,MN与DE的延长线的交点为F2,如图.
∵M、N分别是AB、AC的中点,
∴MN∥BC,MN=
BC,
∴∠MF1B=∠CBF1.
∵点I为△ABC的内心,
∴BI平分∠ABC,
∴∠ABF1=∠CBF1.
∴∠MF1B=∠ABF1,
∴MF1=MB.
∵内切圆⊙I与边BC、CA、AB相切于D、E、G,
∴AG=AE,BG=BD,CD=CE,
∴2CE=AC+BC-AB,
∴CE=
.
∵MN∥BC,CD=CE,∠NEF2=∠CED
∴∠NF2E=∠EDC=∠DEC=∠NEF2,
∴NF2=NE,
∴MF2=MN+NF2=MN+NE=
+NC-EC
=
+
-
=
=MB=MF1,
∴点F1与点F2重合,
∴MN,BI,DE三线共点.
∵M、N分别是AB、AC的中点,
∴MN∥BC,MN=
| 1 |
| 2 |
∴∠MF1B=∠CBF1.
∵点I为△ABC的内心,
∴BI平分∠ABC,
∴∠ABF1=∠CBF1.

∴∠MF1B=∠ABF1,
∴MF1=MB.
∵内切圆⊙I与边BC、CA、AB相切于D、E、G,
∴AG=AE,BG=BD,CD=CE,
∴2CE=AC+BC-AB,
∴CE=
| AC+BC-AB |
| 2 |
∵MN∥BC,CD=CE,∠NEF2=∠CED
∴∠NF2E=∠EDC=∠DEC=∠NEF2,
∴NF2=NE,
∴MF2=MN+NF2=MN+NE=
| BC |
| 2 |
=
| BC |
| 2 |
| AC |
| 2 |
| AC+BC-AB |
| 2 |
=
| AB |
| 2 |
∴点F1与点F2重合,
∴MN,BI,DE三线共点.
点评:本题考查了切线长定理、切线的性质、三角形中位线定理、等腰三角形的判定与性质等知识,解决本题的关键是把“证明MN,BI,DE三线共点”转化为证明“MN与BI延长线的交点”与“MN与DE延长线的交点”重合.

练习册系列答案
相关题目
若(2x-y)2+2(2x-y)-3=0,则2x-y的值是( )
| A、1或-3 | B、-1或3 |
| C、1 | D、-3 |
已知|a|=5,则|a-2|的值是( )
| A、3 | B、-3或7 |
| C、5或-7 | D、7或3 |
以下各组数为边长的三角形中,能组成直角三角形的是( )
| A、1,2,3 |
| B、2,3,4 |
| C、4,5,6 |
| D、5,12,13 |
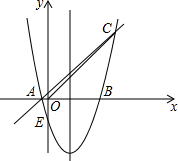 如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).
如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m). 如图,如果AB=AC,可补充的条件是
如图,如果AB=AC,可补充的条件是
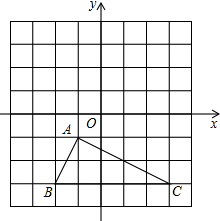 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.