��Ŀ����
�ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1����ֱ�dzߵĶ������P����ֱ�dzߵ����߷ֱ�AB��BC�ڵ�E��F������EF����ͼ�٣���
��1������E���B�غ�ʱ����Fǡ�����C�غϣ���ͼ�ڣ���PC�ij�Ϊ ��
��2��̽������ֱ�ߴ�ͼ���е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E�͵�A�غ�ʱֹͣ������������У���ͼ���Ǹù��̵�ij��ʱ�̣�������۲졢���룬�����
��ֵ�Ƿ����仯��������䣬ֻ��ֱ��д����ֵ����������仯�����˵�����ɣ�
��3������PB����ͼ�ۣ���ֱ�dz���ת�����У����ŵ�E��Fλ�õĸı䣬���������֣���BE=PEʱ��
EF��ֱƽ��PB������������ʱ��E�ھ���A���Զ����

��1������E���B�غ�ʱ����Fǡ�����C�غϣ���ͼ�ڣ���PC�ij�Ϊ
��2��̽������ֱ�ߴ�ͼ���е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E�͵�A�غ�ʱֹͣ������������У���ͼ���Ǹù��̵�ij��ʱ�̣�������۲졢���룬�����
| PF |
| PE |
��3������PB����ͼ�ۣ���ֱ�dz���ת�����У����ŵ�E��Fλ�õĸı䣬���������֣���BE=PEʱ��
EF��ֱƽ��PB������������ʱ��E�ھ���A���Զ����

���㣺���α任�ۺ���
ר�⣺
��������1���ɹ��ɶ�����PB�����û����ϵ֤����APB�ס�DCP���������Ʊ���PC��
��2��
��ֵ���䣮����Ϊ����F��FG��AD������ΪG��ͬ��1���ķ���֤����APE�ס�GFP�������Ʊ�
=
=
=2��������������Ǻ����Ķ�����ֵ��
��3�����ݹ��ɶ������ɵù���x��һԪһ�η��̣��ⷽ�̣��ɵô𰸣�
��2��
| PF |
| PE |
| PF |
| PE |
| GF |
| AP |
| 2 |
| 1 |
��3�����ݹ��ɶ������ɵù���x��һԪһ�η��̣��ⷽ�̣��ɵô𰸣�
�����1���⣺ �ھ���ABCD�У���A=��D=90�㣬
�ھ���ABCD�У���A=��D=90�㣬
AP=1��CD=AB=2����PB=
��
���ABP+��APB=90�㣬
�֡ߡ�BPC=90�㣬
���APB+��DPC=90�㣬
���ABP=��DPC��
���APB�ס�DCP��
��
=
����
=
��
��PC=2
��
�ʴ�Ϊ��2
��2��
��ֵ���䣮����Ϊ��
֤���� ��F��FG��AD������ΪG��
��F��FG��AD������ΪG��
���ı���ABFG�Ǿ��Σ�
���A=��PGF=90�㣬GF=AB=2��
���AEP+��APE=90�㣬
�֡ߡ�EPF=90�㣬
���APE+��GPF=90�㣬
���AEP=��GPF��
���APE�ס�GFP��
��
=
=
=2��
��Rt��EPF��tan��PEF=
=2��
��
��ֵ���䣬
�ʴ�Ϊ��
��ֵ���䣻
��3���⣺ ��AE=x��BE=2-x��
��AE=x��BE=2-x��
��PE=BE=2-x��
��Rt��APE�У��ɹ��ɶ�������
AE2+AP2=PE2��
��x2+1=��2-x��2��
���x=
��
��E�ھ���A��
ʱ��EF��ֱƽ��PB��
 �ھ���ABCD�У���A=��D=90�㣬
�ھ���ABCD�У���A=��D=90�㣬AP=1��CD=AB=2����PB=
| 5 |
���ABP+��APB=90�㣬
�֡ߡ�BPC=90�㣬
���APB+��DPC=90�㣬
���ABP=��DPC��
���APB�ס�DCP��
��
| AP |
| CD |
| PB |
| PC |
| 1 |
| 2 |
| ||
| PC |
��PC=2
| 5 |
�ʴ�Ϊ��2
| 5 |
��2��
| PF |
| PE |
֤����
 ��F��FG��AD������ΪG��
��F��FG��AD������ΪG�����ı���ABFG�Ǿ��Σ�
���A=��PGF=90�㣬GF=AB=2��
���AEP+��APE=90�㣬
�֡ߡ�EPF=90�㣬
���APE+��GPF=90�㣬
���AEP=��GPF��
���APE�ס�GFP��
��
| PE |
| PE |
| GF |
| AP |
| 2 |
| 1 |
��Rt��EPF��tan��PEF=
| PF |
| PE |
��
| PF |
| PE |
�ʴ�Ϊ��
| PF |
| PE |
��3���⣺
 ��AE=x��BE=2-x��
��AE=x��BE=2-x����PE=BE=2-x��
��Rt��APE�У��ɹ��ɶ�������
AE2+AP2=PE2��
��x2+1=��2-x��2��
���x=
| 3 |
| 4 |
��E�ھ���A��
| 3 |
| 4 |
���������⿼�������������ε��ж������ʣ����ε����ʣ��Լ���ֱ�������Σ����ɶ���������Ĺؼ������û����ϵ֤�����������Σ�

��ϰ��ϵ�д�
 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
�����Ŀ
 ��ͼ��AB�ǡ�Oֱ������CD��AB�ཻ�ڵ�E����ACD=52�㣬��ADC=26�㣮���CEB�Ķ�����
��ͼ��AB�ǡ�Oֱ������CD��AB�ཻ�ڵ�E����ACD=52�㣬��ADC=26�㣮���CEB�Ķ�����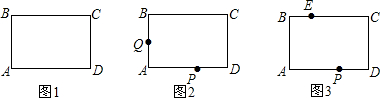
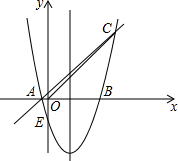 ��ͼ���Գ���Ϊx=1��������y=x2+bx+c��ͼ����x���һ������ΪB��3��0������һ������ΪA����y�ύ�ڵ�E���Ҿ�����C��4��m����
��ͼ���Գ���Ϊx=1��������y=x2+bx+c��ͼ����x���һ������ΪB��3��0������һ������ΪA����y�ύ�ڵ�E���Ҿ�����C��4��m����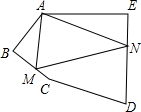 ��ͼ���������ABCDE�У���BAE=120�㣬��B=��E=90�㣬AB=BC��AE=DE���ڱ�BC��DE�Ϸֱ���һ��M��N��ʹ�á�AMN�ܳ���С�����AMN+��ANM=
��ͼ���������ABCDE�У���BAE=120�㣬��B=��E=90�㣬AB=BC��AE=DE���ڱ�BC��DE�Ϸֱ���һ��M��N��ʹ�á�AMN�ܳ���С�����AMN+��ANM= ijˮ����ֲ��ȥ�깲ժ��һ������4000kg�����ƻ��ڽ����ij������ȫ���۳��������ܼ��ڵ�����Ӱ�죬ÿǧ��һ�����ٵ���ƽ���ۼ���ͼ��ʾ��ͼ�и�����ͬһֱ���ϣ����Խ���һ�·ݿ�ʼ������ÿ�ౣ��һ���½�����200kg��ͬʱ��Ҫ����0.02Ԫ/kg�ı���ѣ�
ijˮ����ֲ��ȥ�깲ժ��һ������4000kg�����ƻ��ڽ����ij������ȫ���۳��������ܼ��ڵ�����Ӱ�죬ÿǧ��һ�����ٵ���ƽ���ۼ���ͼ��ʾ��ͼ�и�����ͬһֱ���ϣ����Խ���һ�·ݿ�ʼ������ÿ�ౣ��һ���½�����200kg��ͬʱ��Ҫ����0.02Ԫ/kg�ı���ѣ� ��ͼ����֪��ABC�У�ADΪBC�������ߣ���C����һ��ֱ�߽�AD��E����AB��F����֤��AE��ED=2AF��FB��
��ͼ����֪��ABC�У�ADΪBC�������ߣ���C����һ��ֱ�߽�AD��E����AB��F����֤��AE��ED=2AF��FB��