题目内容
16. 如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.
如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.(1)求证:CE=DF.
(2)连接DE、EF,证明四边形CDEF为矩形.
分析 (1)利用三角形中位线定理,直角三角形斜边中线的性质即可证明.
(2)只要证明四边形CDEF是平行四边形即可.
解答 (1)证明: ∵AD=DC,CF=FB,
∵AD=DC,CF=FB,
∴DF=$\frac{1}{2}$AB,
∵△ACB是直角三角形,AE=EB,
∴CE=$\frac{1}{2}$AB,
∴CE=DF.
(2)证明:连接DE、EF,如图所示.
∵D、E、F分别是AC、AB、BC的中点,
∴DE、EF为△ABC的中位线,
∴DE∥BC,EF∥AC,
∴四边形CDEF为平行四边形.
∵∠ACB=90°,
∴平行四边形CDEF为矩形.
点评 本题考查三角形中位线定理、直角三角形斜边中线的性质、平行四边形的判定.矩形的判定等知识,解题的关键是熟练掌握三角形中位线定理,直角三角形斜边中线的性质,掌握矩形的判定方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.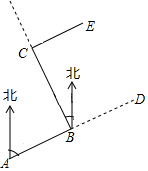 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 105° |
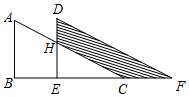 如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.
如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.



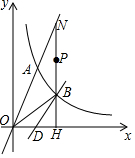 直线y=x-1交x轴于D点,交双曲线y=$\frac{k}{x}$(k>0)于B点,直线y=2x交双曲线y=$\frac{k}{x}$(k>0)于A点.
直线y=x-1交x轴于D点,交双曲线y=$\frac{k}{x}$(k>0)于B点,直线y=2x交双曲线y=$\frac{k}{x}$(k>0)于A点.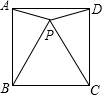 如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD=150°,S△APB=4.
如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD=150°,S△APB=4.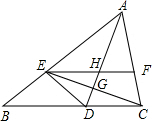 如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.