题目内容
5.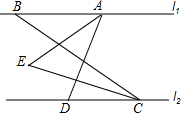 如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.
如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.(1)试说明∠ADC=2∠BAE;
(2)若∠ADC=70°,∠ABC=n°,求∠AEC的度数(用含n的式子表示)
分析 (1)由l1∥l2知∠BAD=∠ADC,根据AE平分∠BAD知∠ADC=∠BAD=2∠BAE;
(2)作EF∥l1,可得∠BAE=∠AEF=$\frac{1}{2}$∠ADC=35°,再由l1∥l2知∠ABC=∠BCD=n°,结合CE平分∠BCD知∠DCE=$\frac{1}{2}$∠BCD=$\frac{1}{2}$n°,根据l1∥l2、EF∥l1知EF∥l2,可得∠CEF=∠DCE,根据∠AEC=∠AEF+∠CEF可得答案.
解答 解:(1)∵l1∥l2,
∴∠BAD=∠ADC,
∵AE平分∠BAD,
∴∠BAD=2∠BAE,
∴∠ADC=2∠BAE;
(2)过点E作EF∥l1,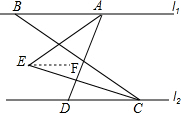
则∠BAE=∠AEF,
∵∠ADC=70°,
由(1)知∠BAE=$\frac{1}{2}$∠ADC=35°,
∴∠AEF=35°,
∵l1∥l2,
∴∠ABC=∠BCD=n°,
∵CE平分∠BCD,
∴∠DCE=$\frac{1}{2}$∠BCD=$\frac{1}{2}$n°,
又∵l1∥l2、EF∥l1,
∴EF∥l2,
∴∠CEF=∠DCE=$\frac{1}{2}$n°,
∴∠AEC=∠AEF+∠CEF=35°+$\frac{1}{2}$n°.
点评 本题主要考查平行线的判定与性质及角平分线,熟练掌握平行线的判定及性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列判断:
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.若方程组$\left\{\begin{array}{l}{x-y=k+3}\\{2x+y=5k}\end{array}\right.$的解满足x+y<2,则k的取值范围是( )
| A. | k<-1 | B. | 1<k<2 | C. | k<1 | D. | -1<k<1 |
15.下面四个二次根式,化简后可以与$\sqrt{3}$进行合并的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{12}$ |
 如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( ) 用固定的速度往如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )
用固定的速度往如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )


