题目内容
17. 用固定的速度往如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )
用固定的速度往如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 结合瓶子的结构和题意知,容器的截面积越大水的高度变化慢、反之变化的快,再由图象越平缓就是变化越慢、图象陡就是变化快来判断.
解答 解:因瓶子下面窄上面宽,
且相同的时间内注入的水量相同,
所以下面的高度增加的快,
上面增加的慢,
即图象应越来越缓,
分析四个图象只有C符合要求.
故选A.
点评 本题考查了函数的图象,利用数形结合思想,对于此题没有必要求容器中水面的高度h和时间t之间的函数解析式,因此可结合几何体和图象作定性分析,即充分利用数形结合思想.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.下列依次给出的点的坐标(0,3),(1,1),(2,-1),(3,-3),…,依此规律,则第2017个点的坐标为( )
| A. | (2017,-2015) | B. | (2016,-2014) | C. | (2016,-4029) | D. | (2016,-4031) |
9.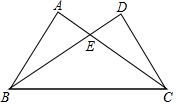 如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
 如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )| A. | ∠D=60° | B. | ∠DBC=40° | C. | AC=DB | D. | BE=10 |
6.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
①3cm,4cm,5cm
②8cm,7cm,15cm
③13cm,12cm,20cm
④5cm,5cm,11cm.
①3cm,4cm,5cm
②8cm,7cm,15cm
③13cm,12cm,20cm
④5cm,5cm,11cm.
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
7.在实数-2,0,-$\sqrt{3}$,1中,最小的数是( )
| A. | -2 | B. | 0 | C. | -$\sqrt{3}$ | D. | 1 |
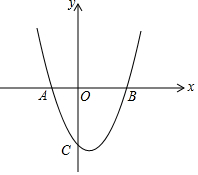 如图,在平面直角坐标系中,已知抛物线y=$\frac{3}{2}$x2+bx+c与x轴交于A(-1,0),B(2,0)两点,与y轴交于点C.
如图,在平面直角坐标系中,已知抛物线y=$\frac{3}{2}$x2+bx+c与x轴交于A(-1,0),B(2,0)两点,与y轴交于点C.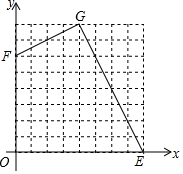 如图,在平面直角坐标系xOy中,E(8,0),F(0,6).
如图,在平面直角坐标系xOy中,E(8,0),F(0,6).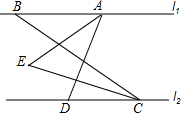 如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.
如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.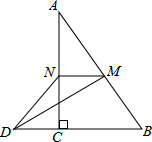 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=$\frac{1}{2}$BC,连接DM,DN,MN,若AB=6,则DN=3.
如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=$\frac{1}{2}$BC,连接DM,DN,MN,若AB=6,则DN=3.